摘要： 解:(1)证明:面PBC⊥面PAC. -----------------------4分知:BC⊥面PAC二面角P―BC―A平面角为∠PCA=.则AH⊥PC.易知.AH⊥面PBC,∴BH为AB在面PBC上射影.∴∠ABH即为AB与面PBC所成的角. ----6分可求:AH=AC?sin=故在△AHB中.sin∠ABH= ----8分(3)设P到面ABH的距离为d.则 =d=??AH?BH?d=???d.
网址：http://m.1010jiajiao.com/timu_id_134610[举报]
已知正方体ABCD－A1B1C1D1，
O是底面ABCD对角线的交点.
（1）求证：A1C⊥平面AB1D1；
（2）求
.
【解析】（1）证明线面垂直，需要证明直线垂直这个平面内的两条相交直线，本题只需证：
即可.
（2）可以利用向量法，也可以根据平面A1ACC1与平面AB1D1垂直，可知取B1D1的中点E，则
就是直线AC与平面AB1D1所成的角.然后解三角形即可.
查看习题详情和答案>>
如图，AC为圆O的直径，AP⊥圆O，PA=AB=BC．
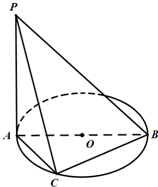如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一动点．（1）证明：面PAC⊥面PBC；
（2）若PA=AB=2，则当直线PC与平面ABC所成角正切值为
| 2 |
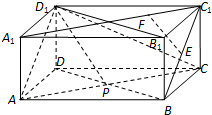如图，在长方体ABCD-A1B1C1D1中，AB=AD=2．
如图，正方形ABCD和直角梯形ABMN所在平面相互垂直，AN∥BM，∠ABM=90°，AN=AD=