题目内容
 如图,正方形ABCD和直角梯形ABMN所在平面相互垂直,AN∥BM,∠ABM=90°,AN=AD=
如图,正方形ABCD和直角梯形ABMN所在平面相互垂直,AN∥BM,∠ABM=90°,AN=AD=| 1 | 2 |
(1)证明NP∥面ABCD;
(II)证明:MN⊥NC;
(III)求三棱锥M-BPN的体积.
分析:(I)取BC中点Q,连接PQ,AQ,证明NP∥AQ.说明AQ?平面ABCD,且NP?平面ABCD,即可证明NP∥平面ABCD;
(II)先证明CB⊥MN,由勾股定理得出MN⊥NB,即可证明MN⊥平面BNC,从而有MN⊥NC;
(III)取MB的中点,连接PE,先证得PE即为三棱锥M-PBN的高,再求出底面的面积、高,即可求三棱锥的体积.
(II)先证明CB⊥MN,由勾股定理得出MN⊥NB,即可证明MN⊥平面BNC,从而有MN⊥NC;
(III)取MB的中点,连接PE,先证得PE即为三棱锥M-PBN的高,再求出底面的面积、高,即可求三棱锥的体积.
解答: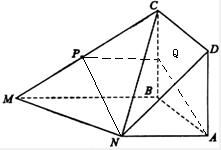 解:(I)证明:取BC中点Q,P是MC的中点,连接PQ,AQ.
解:(I)证明:取BC中点Q,P是MC的中点,连接PQ,AQ.
所以PQ∥BM,AN∥BM,且PQ=AN.
所以四边形ANPQ为平行四边形.
所以NP∥AQ. (4分)
又因为AQ?平面ABCD,且NP?平面ABCD,
所以NP∥平面ABCD. (4分)
(II)证明:在正方形BCD中,CB⊥AB.
又因为平面ABMN⊥平面ABCD,所以CB⊥平面ABMN.
所以CB⊥MN. (6分)
在直角梯形ABMN中,AN=AB=1,可得NB=MN=
AB,
所以BN2+MN2=MB2.
所以MN⊥NB.
所以MN⊥平面BNC,
所以MN⊥NC. (8分)
(III)取MB的中点,连接PE,则PE∥BC,又BC∥AD,AD⊥面ABMN,
所以BC⊥面ABMN,∴PE⊥面ABMN,
∴PE即为三棱锥M-PBN的高,且PE=
BC=
•
∴VM-BPN=
S△BPN•PE=
×
×2×1×
=
•(12分)
 解:(I)证明:取BC中点Q,P是MC的中点,连接PQ,AQ.
解:(I)证明:取BC中点Q,P是MC的中点,连接PQ,AQ.所以PQ∥BM,AN∥BM,且PQ=AN.
所以四边形ANPQ为平行四边形.
所以NP∥AQ. (4分)
又因为AQ?平面ABCD,且NP?平面ABCD,
所以NP∥平面ABCD. (4分)
(II)证明:在正方形BCD中,CB⊥AB.
又因为平面ABMN⊥平面ABCD,所以CB⊥平面ABMN.
所以CB⊥MN. (6分)
在直角梯形ABMN中,AN=AB=1,可得NB=MN=
| 2 |
所以BN2+MN2=MB2.
所以MN⊥NB.
所以MN⊥平面BNC,
所以MN⊥NC. (8分)
(III)取MB的中点,连接PE,则PE∥BC,又BC∥AD,AD⊥面ABMN,
所以BC⊥面ABMN,∴PE⊥面ABMN,
∴PE即为三棱锥M-PBN的高,且PE=
| 1 |
| 2 |
| 1 |
| 2 |
∴VM-BPN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题是中档题,考查直线与平面的平行与垂直的证明方法,几何体的体积的解法,考查空间想象能力、计算能力,注意转化思想的应用,判定定理的正确应用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为