Question

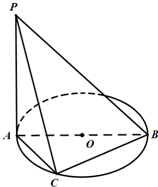如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一动点．
（1）证明：面PAC⊥面PBC；
（2）若PA=AB=2，则当直线PC与平面ABC所成角正切值为

2

时，求直线AB与平面PBC所成角的正弦值．

Answer 1

分析：（1）要证明平面PAC垂直于平面PBC，直线证明平面PBC内的直线BC，垂直平面PAC内的两条相交直线PA、AC即可；
（2）利用直线PC与平面ABC所成角正切值为

2

，求出AC，在直角△PAC中，求出AH，在直角△ABH中，可求AC与平面PBC所成角正弦值．

解答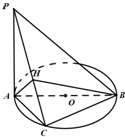：（1）证明：∵PA⊥平面ABC，∴PA⊥BC，
又∵∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∴BC⊥AC．
∵AP∩AC=A，∴BC⊥平面PAC．
∵BC?平面PBC，∴平面PAC⊥平面PBC．
（2）解：如图，过A作AH⊥PC于H，
∵BC⊥平面PAC，∴BC⊥AH，
∵PC∩BC=C，
∴AH⊥平面PBC，则∠ABH即是要求的角．
∵PA⊥平面ABC，∴∠PCA即是PC与平面ABC所成角，
∴tan∠PCA=

PA

AC

=

2

，
又PC=2，∴AC=

2

，
∴在直角△PAC中，AH=

PA•AC

PA2+AC2

=

2 3

3

在直角△ABH中，sin∠ABH=

2 3 3

2

=

3

3

，即AC与平面PBC所成角正弦值为

3

3

．

点评：本题考查平面与平面垂直的判定，考查线面角，考查空间想象能力，逻辑思维能力，属于中档题．