网址:http://m.1010jiajiao.com/timu_id_130198[举报]
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
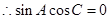

又由 得
得 即
即

又由 得
得 即
即

又
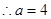 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

查看习题详情和答案>>
在数列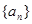 中,
中,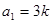 ,其中
,其中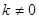 ,对任意
,对任意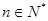 都有:
都有: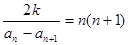 ;(1)求数列
;(1)求数列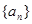 的第2项和第3项;
的第2项和第3项;
(2)求数列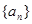 的通项公式
的通项公式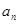 ,假设
,假设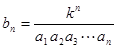 ,试求数列
,试求数列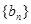 的前
的前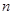 项和
项和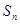 ;
;
(3)若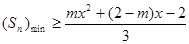 对一切
对一切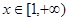 恒成立,求
恒成立,求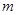 的取值范围。
的取值范围。
【解析】第一问中利用)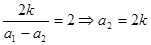 同理得到
同理得到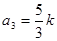
第二问中,由题意得到: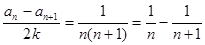
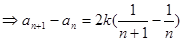
累加法得到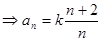
第三问中,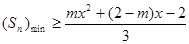 利用恒成立,转化为最小值大于等于即可。得到范围。
利用恒成立,转化为最小值大于等于即可。得到范围。
(1)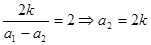 同理得到
同理得到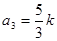 ……2分
……2分
(2)由题意得到: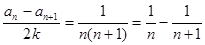
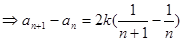
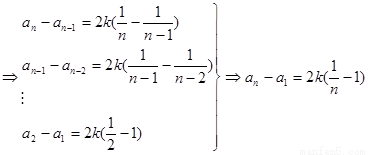 又
又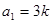
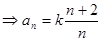 ……5分
……5分
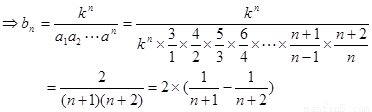
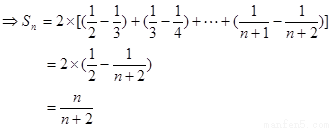 ……8分
……8分
(3)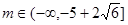
查看习题详情和答案>>
已知m>1,直线 ,椭圆C:
,椭圆C: ,
, 、
、 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.
(Ⅰ)当直线过右焦点 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A
 、△B
、△B
 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
【解析】第一问中因为直线 经过点
经过点 (
( ,0),所以
,0),所以 =
= ,得
,得 .又因为m>1,所以
.又因为m>1,所以 ,故直线的方程为
,故直线的方程为
第二问中设 ,由
,由 ,消去x,得
,消去x,得 ,
,
则由 ,知
,知 <8,且有
<8,且有
由题意知O为
 的中点.由
的中点.由 可知
可知 从而
从而 ,设M是GH的中点,则M(
,设M是GH的中点,则M( ).
).
由题意可知,2|MO|<|GH|,得到范围
查看习题详情和答案>>
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积。
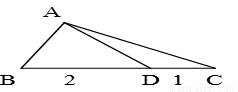
【解析】本试题主要考查了余弦定理的运用。利用由题意得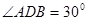 ,
,

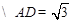 ,
,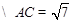 并且
并且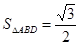 有
有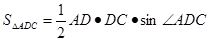 得到结论。
得到结论。
解:(Ⅰ)由题意得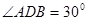 ,
,
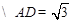 ………1分
………1分 …………1分
…………1分
(Ⅱ)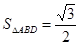 ………………1分
………………1分
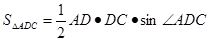
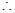
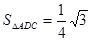

查看习题详情和答案>>
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
查看习题详情和答案>>