题目内容
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
【答案】
(Ⅰ)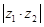 =
=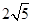 (Ⅱ)见解析
(Ⅱ)见解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
关于复数z=
,下列说法中正确的是( )
| (1+i)2 |
| 1-i |
| A、在复平面内复数z对应的点在第一象限 | ||
B、复数z的共轭复数
| ||
| C、若复数z1=z+b(b∈R)为纯虚数,则b=1 | ||
| D、设a,b为复数z的实部和虚部,则点(a,b)在以原点为圆心,半径为1的圆上 |
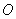 是原点,
是原点,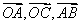 表示的复数分别为
表示的复数分别为 那么
那么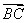 表示的复数为 ;
表示的复数为 ;