网址:http://m.1010jiajiao.com/timu_id_117182[举报]
一、填空题(每题5分,理科总分55分、文科总分60分):
1. 2009.04.files/image283.gif) ; 2.
理:2;文:
; 2.
理:2;文:2009.04.files/image285.gif) ; 3. 理:1.885;文:2;
; 3. 理:1.885;文:2;
4. 理:2009.04.files/image287.gif) ;文:1.885; 5. 理:
;文:1.885; 5. 理:2009.04.files/image289.gif) ;文:4; 6. 理:
;文:4; 6. 理:2009.04.files/image291.gif) ;文:
;文:2009.04.files/image287.gif) ;
;
7. 理:2009.04.files/image293.gif) ;文:
;文:2009.04.files/image289.gif) ; 8. 理:
; 8. 理:2009.04.files/image130.gif) ;文:6; 9. 理:
;文:6; 9. 理:2009.04.files/image296.gif) ;文:
;文:2009.04.files/image298.gif) ;
;
10. 理:1; 文:2009.04.files/image130.gif) ; 11. 理:
; 11. 理:2009.04.files/image300.gif) ;文:
;文:2009.04.files/image296.gif) ; 12. 文:
; 12. 文:2009.04.files/image300.gif) ;
;
二、选择题(每题4分,总分16分):
题号
理12;文13
理13;文14
理:14;文:15
理15;文:16
答案
A
C
B
C
三、解答题:
16.(理,满分12分)
解:因为抛物线的焦点2009.04.files/image166.gif) 的坐标为
的坐标为2009.04.files/image303.gif) ,设
,设2009.04.files/image305.gif) 、
、2009.04.files/image307.gif) ,
,
由条件,则直线2009.04.files/image170.gif) 的方程为
的方程为2009.04.files/image310.gif) ,
,
代入抛物线方程2009.04.files/image164.gif) ,可得
,可得2009.04.files/image312.gif) ,则
,则2009.04.files/image314.gif) .
.
于是,2009.04.files/image316.gif) .
.
…2
…4
…8
…12
17.(文,满分12分)
解:因为2009.04.files/image318.gif) ,所以由条件可得
,所以由条件可得2009.04.files/image320.gif) ,
,2009.04.files/image100.gif) .
.
即数列2009.04.files/image114.gif) 是公比
是公比2009.04.files/image323.gif) 的等比数列.
的等比数列.
又2009.04.files/image325.gif) ,
,
所以,2009.04.files/image327.gif) .
.
…4
…6
…8
…12
(理)17.(文)18. (满分14分)
解:因为2009.04.files/image329.gif)
2009.04.files/image331.gif)
所以,2009.04.files/image333.gif)
2009.04.files/image335.gif)
2009.04.files/image337.gif)
即2009.04.files/image339.gif) 或
或2009.04.files/image341.gif) ,
,2009.04.files/image343.gif)
2009.04.files/image345.gif) 或
或2009.04.files/image347.gif) ,
,2009.04.files/image343.gif)
又由2009.04.files/image183.gif) ,即
,即
当2009.04.files/image349.gif) 时,
时,2009.04.files/image351.gif) 或
或2009.04.files/image353.gif) ;当
;当2009.04.files/image355.gif) 时,
时,2009.04.files/image357.gif) 或
或2009.04.files/image359.gif) .
.
所以,集合2009.04.files/image361.gif) .
.
…3
…7
…11
…14
18.(理,满分15分,第1小题6分,第2小题9分)
解:(1)当2009.04.files/image363.gif) 时,
时,2009.04.files/image365.gif)
2009.04.files/image367.gif)
2009.04.files/image369.gif)
故2009.04.files/image371.gif) ,
,2009.04.files/image373.gif) ,所以
,所以2009.04.files/image375.gif) .
.
(2)证:由数学归纳法
(i)当2009.04.files/image377.gif) 时,易知
时,易知2009.04.files/image379.gif) ,为奇数;
,为奇数;
(ii)假设当2009.04.files/image381.gif) 时,
时,2009.04.files/image383.gif) ,其中
,其中2009.04.files/image385.gif) 为奇数;
为奇数;
则当2009.04.files/image387.gif) 时,
时,
2009.04.files/image389.gif)
2009.04.files/image391.gif)
所以2009.04.files/image393.gif) ,又
,又2009.04.files/image395.gif) 、
、2009.04.files/image397.gif) ,所以
,所以2009.04.files/image399.gif) 是偶数,
是偶数,
而由归纳假设知2009.04.files/image385.gif) 是奇数,故
是奇数,故2009.04.files/image402.gif) 也是奇数.
也是奇数.
综上(i)、(ii)可知,2009.04.files/image404.gif) 的值一定是奇数.
的值一定是奇数.
证法二:因为2009.04.files/image406.gif)
当2009.04.files/image408.gif) 为奇数时,
为奇数时,2009.04.files/image410.gif)
则当2009.04.files/image377.gif) 时,
时,2009.04.files/image379.gif) 是奇数;当
是奇数;当2009.04.files/image414.gif) 时,
时,
因为其中2009.04.files/image416.gif) 中必能被2整除,所以为偶数,
中必能被2整除,所以为偶数,
于是,2009.04.files/image410.gif) 必为奇数;
必为奇数;
当2009.04.files/image408.gif) 为偶数时,
为偶数时,2009.04.files/image419.gif)
其中2009.04.files/image421.gif) 均能被2整除,于是
均能被2整除,于是2009.04.files/image404.gif) 必为奇数.
必为奇数.
综上可知,2009.04.files/image096.gif) 各项均为奇数.
各项均为奇数.
…3
…6
…8
…10
…14
…15
…10
…14
…15
19. (文,满分14分)
解:如图,设2009.04.files/image270.gif) 中点为
中点为2009.04.files/image425.gif) ,联结
,联结2009.04.files/image246.gif) 、
、2009.04.files/image428.gif) .
.
2009.04.files/image430.gif) 由题意,
由题意,2009.04.files/image432.gif) ,
,2009.04.files/image434.gif) ,所以
,所以2009.04.files/image436.gif) 为等边三角形,
为等边三角形,
故2009.04.files/image438.gif) ,且
,且2009.04.files/image440.gif) .
.
又2009.04.files/image442.gif) ,
,
所以2009.04.files/image444.gif) .
.
而圆锥体的底面圆面积为2009.04.files/image446.gif) ,
,
所以圆锥体体积2009.04.files/image448.gif) .
.
…3
…8
…10
…14
(理)19. (文)20. (满分16分,第1小题4分,第2小题6分,第3小题6分)
解:(1)由题意,当2009.04.files/image212.gif) 和
和2009.04.files/image214.gif) 之间的距离为
之间的距离为2009.04.files/image212.gif) 应位于
应位于2009.04.files/image264.gif) 上方,
上方,
且此时2009.04.files/image210.gif) 中
中2009.04.files/image212.gif) 边上的高为
边上的高为
2009.04.files/image454.gif) 又因为
又因为2009.04.files/image456.gif) 米,可得
米,可得2009.04.files/image458.gif) 米.
米.
所以,2009.04.files/image460.gif) 平方米,
平方米,
即三角通风窗2009.04.files/image218.gif) 的通风面积为
的通风面积为2009.04.files/image463.gif) 平方米.
平方米.
(2)12009.04.files/image465.gif) 如图(1)所示,当
如图(1)所示,当2009.04.files/image212.gif) 在矩形区域滑动,即
在矩形区域滑动,即2009.04.files/image467.gif) 时,
时,
2009.04.files/image469.gif) 的面积
的面积2009.04.files/image471.gif) ;
;
22009.04.files/image465.gif) 如图(2)所示,当
如图(2)所示,当2009.04.files/image212.gif) 在半圆形区域滑动,即
在半圆形区域滑动,即2009.04.files/image473.gif) 时,
时,
2009.04.files/image474.gif)
2009.04.files/image476.gif) ,故可得
,故可得2009.04.files/image469.gif) 的面积
的面积
2009.04.files/image478.gif)
2009.04.files/image480.gif)
2009.04.files/image482.gif) ;
;
综合可得:
2009.04.files/image484.gif)
(3)12009.04.files/image465.gif) 当
当2009.04.files/image212.gif) 在矩形区域滑动时,
在矩形区域滑动时,2009.04.files/image012.gif) 在区间
在区间2009.04.files/image487.gif) 上单调递减,
上单调递减,
则有2009.04.files/image489.gif) ;
;
22009.04.files/image465.gif) 当
当2009.04.files/image212.gif) 在半圆形区域滑动时,
在半圆形区域滑动时,
2009.04.files/image491.gif) ,
,
等号成立2009.04.files/image493.gif)
2009.04.files/image495.gif) ,
,2009.04.files/image473.gif)
2009.04.files/image493.gif)
2009.04.files/image498.gif) .
.
因而当2009.04.files/image500.gif) (米)时,每个三角通风窗
(米)时,每个三角通风窗2009.04.files/image218.gif) 得到最大通风面积,最大面积为
得到最大通风面积,最大面积为2009.04.files/image503.gif) (平方米).
(平方米).
…2
…4
…6
…9
…10
…12
…15
…16
21(文,满分18分,第1小题5分,第2小题6分,第3小题7分)
解:(1)设右焦点坐标为2009.04.files/image505.gif) (
(2009.04.files/image507.gif) ).
).
因为双曲线C为等轴双曲线,所以其渐近线必为2009.04.files/image509.gif) ,
,
由对称性可知,右焦点2009.04.files/image166.gif) 到两条渐近线距离相等,且
到两条渐近线距离相等,且2009.04.files/image512.gif) .
.
于是可知,2009.04.files/image514.gif) 为等腰直角三角形,则由
为等腰直角三角形,则由2009.04.files/image516.gif)
2009.04.files/image518.gif) ,
,
又由等轴双曲线中,2009.04.files/image520.gif)
2009.04.files/image522.gif) .
.
即,等轴双曲线2009.04.files/image249.gif) 的方程为
的方程为2009.04.files/image525.gif) .
.
(2)设2009.04.files/image305.gif) 、
、2009.04.files/image307.gif) 为双曲线
为双曲线2009.04.files/image249.gif) 直线
直线2009.04.files/image170.gif) 的两个交点.
的两个交点.
因为2009.04.files/image531.gif) ,直线
,直线2009.04.files/image170.gif) 的方向向量为
的方向向量为2009.04.files/image168.gif) ,直线
,直线2009.04.files/image170.gif) 的方程为
的方程为
2009.04.files/image533.gif) .
.
代入双曲线2009.04.files/image249.gif) 的方程
的方程2009.04.files/image525.gif) ,可得
,可得2009.04.files/image535.gif) ,
,
于是有2009.04.files/image537.gif)
而2009.04.files/image539.gif)
2009.04.files/image541.gif) .
.
(3)假设存在定点2009.04.files/image543.gif) ,使
,使2009.04.files/image545.gif) 为常数,其中
为常数,其中2009.04.files/image547.gif) ,
,2009.04.files/image549.gif) 为直线
为直线2009.04.files/image170.gif) 与双曲线
与双曲线2009.04.files/image249.gif) 的两个交点的坐标.
的两个交点的坐标.
①当直线2009.04.files/image170.gif) 与
与2009.04.files/image185.gif) 轴不垂直时,设直线
轴不垂直时,设直线2009.04.files/image170.gif) 的方程为
的方程为2009.04.files/image556.gif)
代入2009.04.files/image525.gif) ,可得
,可得2009.04.files/image558.gif) .
.
由题意可知,2009.04.files/image560.gif) ,则有
,则有2009.04.files/image562.gif) ,
,2009.04.files/image564.gif) .
.
于是,2009.04.files/image566.gif)
2009.04.files/image568.gif)
2009.04.files/image570.gif)
要使2009.04.files/image545.gif) 是与
是与2009.04.files/image572.gif) 无关的常数,当且仅当
无关的常数,当且仅当2009.04.files/image574.gif) ,此时
,此时2009.04.files/image576.gif) .
.
②当直线2009.04.files/image170.gif) 与
与2009.04.files/image185.gif) 轴垂直时,可得点
轴垂直时,可得点2009.04.files/image579.gif) ,
,2009.04.files/image581.gif) ,
,
若2009.04.files/image574.gif) ,
,2009.04.files/image576.gif) 亦为常数.
亦为常数.
综上可知,在2009.04.files/image185.gif) 轴上存在定点
轴上存在定点2009.04.files/image584.gif) ,使
,使2009.04.files/image576.gif) 为常数.
为常数.
…3
…5
…7
…9
…11
…13
…16
…17
…18
20(理,满分22分,第1小题4分,第2小题6分,第3小题12分)
解:(1)解法一:由题意,四边形2009.04.files/image198.gif) 是直角梯形,且
是直角梯形,且2009.04.files/image246.gif) ∥
∥2009.04.files/image270.gif) ,
,
则2009.04.files/image244.gif) 与
与2009.04.files/image246.gif) 所成的角即为
所成的角即为2009.04.files/image588.gif) .
.
因为2009.04.files/image590.gif) ,又
,又2009.04.files/image232.gif) 平面
平面2009.04.files/image198.gif) ,
,
所以2009.04.files/image592.gif) 平面
平面2009.04.files/image594.gif) ,则有
,则有2009.04.files/image596.gif) .
.
因为2009.04.files/image598.gif) ,
,2009.04.files/image438.gif) ,
,
所以2009.04.files/image601.gif) ,则
,则2009.04.files/image603.gif) ,
,
即异面直线2009.04.files/image244.gif) 与
与2009.04.files/image246.gif) 所成角的大小为
所成角的大小为2009.04.files/image605.gif) .
.
解法二:如图,以2009.04.files/image055.gif) 为原点,直线
为原点,直线2009.04.files/image214.gif) 为
为2009.04.files/image185.gif) 轴、直线
轴、直线2009.04.files/image246.gif) 为
为2009.04.files/image611.gif) 轴、直线
轴、直线2009.04.files/image613.gif) 为
为2009.04.files/image615.gif) 轴,
轴,
建立空间直角坐标系.
于是有2009.04.files/image617.gif) 、
、2009.04.files/image619.gif) ,则有
,则有2009.04.files/image621.gif) ,又
,又2009.04.files/image623.gif)
则异面直线2009.04.files/image244.gif) 与
与2009.04.files/image246.gif) 所成角
所成角2009.04.files/image625.gif) 满足
满足2009.04.files/image627.gif) ,
,
所以,异面直线2009.04.files/image244.gif) 与
与
(本题满分13分)
某班几位同学组成研究性学习小组,对![]() 岁的人群随机抽取n人进行了一次日常生活中是否
岁的人群随机抽取n人进行了一次日常生活中是否
具有环保意识的调查. 若生活习惯具有环保意识的称为“环保族”,否则称为 “非环保族”,得到如下统计表:
| 组数 | 分组 | 环保族人数 | 占本组的频率 | 本组占样本的频率 |
| 第一组 |
| 120 | 0.6 | 0.2 |
| 第二组 |
| 195 | p | q |
| 第三组 |
| 100:] | 0.5 | 0.2 |
| 第四组 |
| a | 0.4 | 0.15 |
| 第五组 |
| 30 | 0.3 | 0.1 |
| 第六组 |
| 15 | 0.3 | 0.05 |
(Ⅰ)求q、n、a、p的值;
(Ⅱ)从年龄段在![]() 的“环保族”中采用分层抽样法抽取6人参加户外环保活动,其中选取2人
的“环保族”中采用分层抽样法抽取6人参加户外环保活动,其中选取2人
作为领队,求选取的2名领队中恰有1人年龄在![]() 的概率.
的概率.
(本小题满分12分)
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 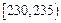 | 8 | 0.16 |
| 第二组 | 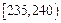 | ① | 0.24 |
| 第三组 | 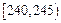 | 15 | ② |
| 第四组 | 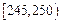 | 10 | 0.20 |
| 第五组 | 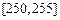 | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率. 查看习题详情和答案>>
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):

 男 女
男 女
 15
7 7 8 9 9 9
15
7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
查看习题详情和答案>>
(本小题满分15分)
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
在选取的40名学生中。
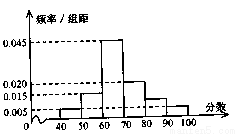
(I)求成绩在区间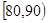 内的学生人数;
内的学生人数;
(II)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率。
查看习题详情和答案>>
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
