摘要:请用0.5毫米黑色墨水签字笔在答题卡上书写作答.在试题卷上书写作答无效.
网址:http://m.1010jiajiao.com/timu_id_11068[举报]
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?(x2=
,当Χ2<2.706时,没有充分的证据判定变量性别有关,当Χ2>2.706时,有90%的把握判定变量性别有关,当Χ2>3.841时,有95%的把握判定变量性别有关,当Χ2>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
查看习题详情和答案>>
| 男性 | 女性 | 合计 | |
| 反感 | 10 | ||
| 不反感 | 8 | ||
| 合计 | 30 |
| 8 |
| 15 |
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?(x2=
| (a+b+c+d)(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
|
|
|
不反感 |
|
8 |
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是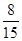 .
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(
当 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
查看习题详情和答案>>
(2012•漳州模拟)本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
已知矩阵A=
有一个属于特征值1的特征向量
=
.
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=
,点O(0,0),M(2,-1),N(0,2),求△OMN在矩阵AB的对应变换作用下所得到的△O'M'N'的面积.
(2)选修4-4:坐标系与参数方程
已知直角坐标系xOy中,直线l的参数方程为
(t为参数).以直角坐标系xOy中的原点O为 极点,x轴的非负半轴为极轴,圆C的极坐标方程为ρ2-4ρcosθ+3=0,
(Ⅰ) 求l的普通方程及C的直角坐标方程;
(Ⅱ) P为圆C上的点,求P到l距离的取值范围.
(3)选修4-5:不等式选讲
已知关于x的不等式:|x-1|+|x+2|≥a2+2|a|-5对任意x∈R恒成立,求实数a的取值范围.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
已知矩阵A=
|
| α |
|
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=
|
(2)选修4-4:坐标系与参数方程
已知直角坐标系xOy中,直线l的参数方程为
|
(Ⅰ) 求l的普通方程及C的直角坐标方程;
(Ⅱ) P为圆C上的点,求P到l距离的取值范围.
(3)选修4-5:不等式选讲
已知关于x的不等式:|x-1|+|x+2|≥a2+2|a|-5对任意x∈R恒成立,求实数a的取值范围.
 本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.(1)选修4-2:矩阵与变换
如图所示:△OAB在伸缩变换M作用下变为△OA1B1.
(i)求矩阵M的特征值及相应的特征向量;
(ii)求逆矩阵M-1以及(M-1)20
(2)选修4-4:坐标系与参数方程.
已知曲线C1的参数方程为
|
|
(i)若将曲线C1与C2上各点的横坐标都缩短为原来的一半,分别得到曲线C1和C2,求出曲线C1和C2的普通方程;
(ii)以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,求过极点且与C2垂直的直线的极坐标方程.
(3)选修4-5:不等式选讲
已知a,b,c为实数,且a+b+c+2-2m=0,a2+
| b 2 |
| 4 |
| c 2 |
| 9 |
(i)求证:a2+
| b 2 |
| 4 |
| c 2 |
| 9 |
| (a+b+c) 2 |
| 14 |
(ii)求实数m的取值范围. 查看习题详情和答案>>