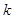题目内容
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
|
|
|
不反感 |
|
8 |
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是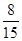 .
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(
当 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
(Ⅰ) 没有充足的理由认为反感“中国式过马路”与性别有关
(Ⅱ)
|
|
0 |
1 |
2 |
|
|
|
|
|
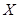 的数学期望为:
的数学期望为: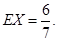
【解析】
试题分析:(Ⅰ)
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
6 |
16 |
|
不反感 |
6 |
8 |
14 |
|
合计 |
16 |
14 |
30 |
由已知数据得: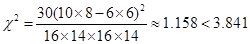 ,
,
所以,没有充足的理由认为反感“中国式过马路”与性别有关.
(Ⅱ)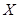 的可能取值为
的可能取值为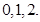
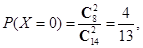
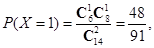
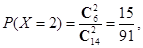
所以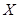 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
|
|
|
|
|
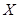 的数学期望为:
的数学期望为: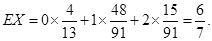
考点:分布列期望与独立性检验
点评:求分布列的步骤:找到随机变量可以取得值,求出各值对应的概率,汇总成分布列;独立性检验的求解步骤:写出分类变量的列联表,求出观测值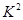 ,比较数据得到结论
,比较数据得到结论

 阅读快车系列答案
阅读快车系列答案“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
|
|
|
不反感 |
|
8 |
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是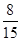 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
|
P(K2>k) |
0.05 |
0.025 |
0.010 |
0.005 |
|
k |
3.841 |
5.024 |
6.635 |
7.879 |
下面的临界值表供参考:
(参考公式:K2=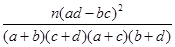 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)"
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
|
|
|
|
不反感 |
|
|
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是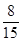 .
.
(Ⅰ)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表 公式:
公式: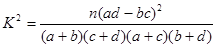 ,
,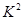 的临界值表:
的临界值表:
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
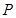
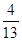
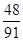
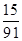
 10
10
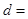 8
8