摘要:21.解:设椭圆方程为(Ⅰ)由已知得∴所求椭圆方程为 .(Ⅱ)解法一:由题意知直线的斜率存在.设直线的方程为由.消去y得关于x的方程:由直线与椭圆相交于A.B两点.解得又由韦达定理得 原点到直线的距离.解法1:对两边平方整理得:(*) ∵. 整理得: 又. 从而的最大值为.此时代入方程(*)得 所以.所求直线方程为:.解法2:令. 则 当且仅当即时. 此时. 所以.所求直线方程为解法二:由题意知直线l的斜率存在且不为零. 设直线l的方程为. 则直线l与x轴的交点. 由解法一知且. 解法1: = . 下同解法一. 解法2: 下同解法一.
网址:http://m.1010jiajiao.com/timu_id_10942[举报]
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
查看习题详情和答案>>
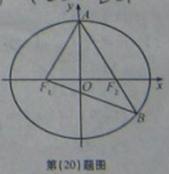
如图,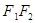 分别是椭圆
分别是椭圆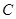 :
: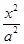 +
+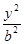 =1(
=1(
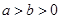 )的左、右焦点,
)的左、右焦点,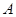 是椭圆
是椭圆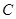 的顶点,
的顶点,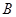 是直线
是直线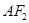 与椭圆
与椭圆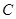 的另一个交点,
的另一个交点,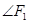
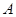
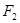 =60°.
=60°.
(Ⅰ)求椭圆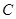 的离心率;
的离心率;
(Ⅱ)已知△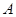
 的面积为40
的面积为40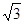 ,求
,求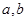 的值.
的值.
【解析】 (Ⅰ)由题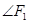
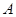
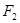 =60°,则
=60°,则 ,即椭圆
,即椭圆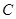 的离心率为
的离心率为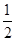 。
。
(Ⅱ)因△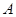
 的面积为40
的面积为40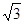 ,设
,设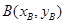 ,又面积公式
,又面积公式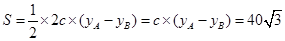 ,又直线
,又直线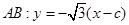 ,
,
又由(Ⅰ)知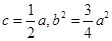 ,联立方程可得
,联立方程可得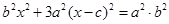 ,整理得
,整理得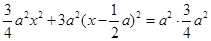 ,解得
,解得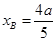 ,
,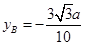 ,所以
,所以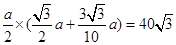 ,解得
,解得 。
。
查看习题详情和答案>>
已知点E、F的坐标分别是(-2,0)、(2,0),直线EP、FP相交于点P,且它们的斜率之积为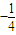 .
.
(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为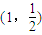 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
查看习题详情和答案>>
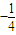 .
.(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为
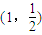 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
查看习题详情和答案>>
已知点E、F的坐标分别是(-2,0)、(2,0),直线EP、FP相交于点P,且它们的斜率之积为-
.
(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为(1,
),试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
查看习题详情和答案>>
| 1 |
| 4 |
(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为(1,
| 1 |
| 2 |
(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
 ,
, 是椭圆
是椭圆
 左右焦点,它的离心率
左右焦点,它的离心率 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为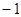
 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求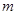 的取值范围。
的取值范围。 得
得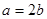 所以椭圆方程可设为:
所以椭圆方程可设为: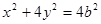 ,然后利用
,然后利用
 得
得



 ,
得
,
得
 得
得