题目内容
已知点E、F的坐标分别是(-2,0)、(2,0),直线EP、FP相交于点P,且它们的斜率之积为-
.
(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为(1,
),试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
| 1 |
| 4 |
(1)求证:点P的轨迹在一个椭圆C上,并写出椭圆C的方程;
(2)设过原点O的直线AB交(1)中的椭圆C于点A、B,定点M的坐标为(1,
| 1 |
| 2 |
(3)反思(2)题的解答,当△MAB的面积取得最大值时,探索(2)题的结论中直线AB的斜率kAB和OM所在直线的斜率kOM之间的关系.由此推广到点M位置的一般情况或椭圆的一般情况(使第(2)题的结论成为推广后的一个特例),试提出一个猜想或设计一个问题,尝试研究解决.
[说明:本小题将根据你所提出的猜想或问题的质量分层评分].
分析:(1)由已知中点E,F的坐标分别是(-2,0)、(2,0),直线EP,FP相交于点P,且它们的斜率之积为 -
.我们设出P(x,y),进而得到x,y之间的关系式,整理后即可知点P的轨迹方程.
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1),联立直线和椭圆的方程,我们可得 x2=
,利用弦定公式,求出AB的长,利用点到直线公式,求出M点直线AB的距离求出AB边的高,可以得到△MAB面积的表达式,进而求出△MAB面积m的取值范围,得到△MAB面积m的,代入可求出对应的k值.
(3)设M(1,4),根据(2)的计算办法,我们易求出,△MAB的面积取得最大值时,并求出此进kOM及kAB的值,验证后,可得猜想不成立.
| 1 |
| 4 |
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1),联立直线和椭圆的方程,我们可得 x2=
| 4 |
| 1+4k2 |
(3)设M(1,4),根据(2)的计算办法,我们易求出,△MAB的面积取得最大值时,并求出此进kOM及kAB的值,验证后,可得猜想不成立.
解答:解:(1)设P(x,y)为轨迹上的动点,由题意
•
=-
⇒x2+4y2=4
即
+y2=1,∴点P的轨迹在椭圆C:
+y2=1上;------------4分
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1)
联立方程 y=kx与
+y2=1
整理可得 x2=
AB=2OA=2
=4
∵M( 1,
)到直线AB的距离d=
S△MAB=
AB•d=
×4
×
=m
则4(1-m2)k2-4k+1-m2=0
则42-4•4(1-m2)•(1-m2)≥0
即(1-m2)2≤1
又由m≥0可得
0≤m≤
即三角形MAB的最大值为
代入4(1-m2)k2-4k+1-m2=0得
k=-
(3)说明:本小题共(8分),建议根据学生提出的问题或猜想的质量划分为三档,其中:
(Ⅰ)此档最高得分(4分),若学生提出诸如:
“设点M(1,b)(ab≠0)为椭圆C:
+y2=1内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点,当且仅当kOM=-kAB时,△MAB的面积取得最大值.此推广不充分,且为假命题的猜想,但能举出反例否定之,则最高得(4分);
若提出的猜想或问题质量不高,则无论能否自行解决,最高得(2分).
(Ⅱ)此档最高得分(6分),若学生的猜想或设计的问题能将点M的位置推广到一般情况或者能将椭圆方程推广到一般情况(即推广了其中一个条件),则可得(4分);
若能分析“kOM=-kAB”为假命题,并能进一步尝试发现斜率kAB和kOM之间的关系(但无明确结论),则最高可得(5分);
学生在自行解决推广其中一个条件的问题中,若能发现kAB和kOM之间的规律(本质规律参考满分一档的解答)或完整解答自己提出的推广问题,则可得(6分).
(Ⅲ)最高得分(8分),若学生能提出较一般化的推广,例如:
试问1:“设点M(m,n)(mn≠0)和椭圆C:
+
=1(a>0,b>0),若过椭圆C中心的直线AB与椭圆分别交于A、B两点,试验证:当△MAB的面积取得最大值时,直线AB的泄率kAB和OM所在直线的斜率kOM满足kAB•kOM=-
”(或其等价命题)则可得(6分);
试问2:“设点M(m,n)(mn≠0)和椭圆C:
+
=1(a>0,b>0),若过椭圆C中心的直线AB与椭圆分别交于A、B两点,试求出当△MAB的面积取得最大值时,直线AB的泄率kAB和OM所在直线的斜率kOM满足的关系式”则可得(5分);
若能找到本质规律并给予证明,则得满分(8分).现给出设问1的一种证明:
证明:设M(m,n)(mn≠0),由椭圆的对称性,可设A(acosθ,bsinθ),点A到直线OM的距离为d,由此OM所在直线方程为nx-my=0,∴d=
=
|sin(θ+φ)|,
其中
,可得tanφ=-
要使d取得最大值,则必有sin(θ+φ)=±1,即θ+φ=kπ+
,k∈Z∴此时必有θ=kπ+
-φ,k∈Z,由题设,当d取得最大值时,kAB=
tanθ=
•tan(kπ+
-φ)=
•cotφ=
•(
)=-
∴此时kAB•kOM=-
•
=-
,
可以验证,在第(2)题条件下,kAB•kOM=-
是以上结论的一个特例.
| y |
| x+2 |
| y |
| x-2 |
| 1 |
| 4 |
即
| x2 |
| 4 |
| x2 |
| 4 |
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1)
联立方程 y=kx与
| x2 |
| 4 |
整理可得 x2=
| 4 |
| 1+4k2 |
AB=2OA=2
| (1+k2)x12 |
|
∵M( 1,
| 1 |
| 2 |
|k-
| ||
|
S△MAB=
| 1 |
| 2 |
| 1 |
| 2 |
|
|k-
| ||
|
则4(1-m2)k2-4k+1-m2=0
则42-4•4(1-m2)•(1-m2)≥0
即(1-m2)2≤1
又由m≥0可得
0≤m≤
| 2 |
即三角形MAB的最大值为
| 2 |
代入4(1-m2)k2-4k+1-m2=0得
k=-
| 1 |
| 2 |
(3)说明:本小题共(8分),建议根据学生提出的问题或猜想的质量划分为三档,其中:
(Ⅰ)此档最高得分(4分),若学生提出诸如:
“设点M(1,b)(ab≠0)为椭圆C:
| x2 |
| 4 |
若提出的猜想或问题质量不高,则无论能否自行解决,最高得(2分).
(Ⅱ)此档最高得分(6分),若学生的猜想或设计的问题能将点M的位置推广到一般情况或者能将椭圆方程推广到一般情况(即推广了其中一个条件),则可得(4分);
若能分析“kOM=-kAB”为假命题,并能进一步尝试发现斜率kAB和kOM之间的关系(但无明确结论),则最高可得(5分);
学生在自行解决推广其中一个条件的问题中,若能发现kAB和kOM之间的规律(本质规律参考满分一档的解答)或完整解答自己提出的推广问题,则可得(6分).
(Ⅲ)最高得分(8分),若学生能提出较一般化的推广,例如:
试问1:“设点M(m,n)(mn≠0)和椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
试问2:“设点M(m,n)(mn≠0)和椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
若能找到本质规律并给予证明,则得满分(8分).现给出设问1的一种证明:
证明:设M(m,n)(mn≠0),由椭圆的对称性,可设A(acosθ,bsinθ),点A到直线OM的距离为d,由此OM所在直线方程为nx-my=0,∴d=
| |ancosθ-bmsinθ| | ||
|
|
其中
|
| an |
| bm |
要使d取得最大值,则必有sin(θ+φ)=±1,即θ+φ=kπ+
| π |
| 2 |
| π |
| 2 |
| b |
| a |
| b |
| a |
| π |
| 2 |
| b |
| a |
| b |
| a |
| -bm |
| an |
| b2m |
| a2n |
| b2m |
| a2n |
| n |
| m |
| b2 |
| a2 |
可以验证,在第(2)题条件下,kAB•kOM=-
| 1 |
| 4 |
点评:本题考查的知识点是直线与圆锥曲线的综合问题,其中(1)的关键是分别求出两条直线的斜率,进而得到P点横、纵坐标的关系式,(2)的关键是得到△MAB面积的表达式,(3)中正面证明比较麻烦,可以举出一反例,推反前面的猜想.

练习册系列答案
相关题目
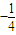 .
.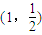 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;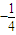 .
.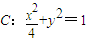 上;
上;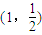 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;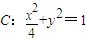 内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.