摘要：如图1所示.在静止的点电荷+Q所产生的电场中.有与+Q共面的A.B.C三点.且B.C处于以+Q为圆心的同一圆周上.设A.B.C三点的电场强度大小分别为EA.EB.EC.电势分别为φA.φB.φC.则下列判断正确的是:
网址：http://m.1010jiajiao.com/timu_id_1083478[举报]
如图所示，在绝缘水平面上的P点放置一个质量为mA=0.02kg的带负电滑块A，带电荷量q=1.0×10-6C．在A的左边相距l=0.9m的Q点放置一个不带电的滑块B，质量为mB=0.04kg，滑块B距左边竖直绝缘墙壁s=0.15m．在水平面上方空间加一方向水平向右的匀强电场，电场强度为E=4.0×105N/C，使A由静止释放后向左滑动并与B发生碰撞，碰撞的时间极短，碰撞后两滑块结合在一起共同运动，与墙壁发生碰撞时没有机械能损失，两滑块都可以视为质点．已知水平面OQ部分粗糙，其余部分光滑，两滑块与粗糙水平面OQ间的动摩擦因数均为μ=0.50，假设最大静摩擦力等于滑动摩擦力，取g=10m/s2．求：（1）A经过多少时间与B相碰？相碰结合后的速度是多少？
（2）AB与墙壁碰撞后在水平面上滑行的过程中，离开墙壁的最大距离是多少？
（3）A、B相碰结合后的运动过程中，由于摩擦而产生的热是多少？通过的总路程是多少？
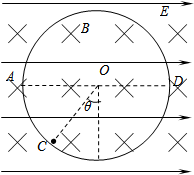如图所示，固定的光滑绝缘圆形轨道竖直放置，处于水平方向的匀强电场和匀强磁场中．已知圆形轨道半径R=2.00m，AD为其水平直径．磁感应强度B=1.00T，方向垂直于纸面向内，电场强度E=1.00×102V/m，方向水平向右．一个质量m=4.00×10-2kg的小球（可视为质点）在轨道上的C点恰好处于静止状态，OC与竖直直径的夹角θ=37°（g取10m/s2，sin37°=0.6，计算结果要求保留三位有效数字）（1）求小球带何种电荷，电荷量q是多少？
（2）现将电场突然反向，但强弱不变，因电场的变化而产生的磁场可忽略不计，小球始终在圆弧轨道上运动，试求在小球运动过程中与初始位置的电势差最大值Um是多少？对轨道的最大压力是多大？
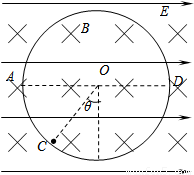
如图所示，固定的光滑绝缘圆形轨道竖直放置，处于水平方向的匀强电场和匀强磁场中．已知圆形轨道半径R=2.00m，AD为其水平直径．磁感应强度B=1.00T，方向垂直于纸面向内，电场强度E=1.00×102V/m，方向水平向右．一个质量m=4.00×10-2kg的小球（可视为质点）在轨道上的C点恰好处于静止状态，OC与竖直直径的夹角θ=37°（g取10m/s2，sin37°=0.6，计算结果要求保留三位有效数字）
（1）求小球带何种电荷，电荷量q是多少？
（2）现将电场突然反向，但强弱不变，因电场的变化而产生的磁场可忽略不计，小球始终在圆弧轨道上运动，试求在小球运动过程中与初始位置的电势差最大值Um是多少？对轨道的最大压力是多大？
查看习题详情和答案>>
（1）求小球带何种电荷，电荷量q是多少？
（2）现将电场突然反向，但强弱不变，因电场的变化而产生的磁场可忽略不计，小球始终在圆弧轨道上运动，试求在小球运动过程中与初始位置的电势差最大值Um是多少？对轨道的最大压力是多大？
查看习题详情和答案>>
（18分）如图所示，水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0，不计电阻的导体棒ab静置在导轨的左端MP处，并与MN垂直．以导轨PQ的左端为坐标原点O，建立直角坐标系xOy，Ox轴沿PQ方向．每根导轨单位长度的电阻为r．垂直于导轨平面的非匀强磁场磁感应强度在y轴方向不变，在x轴方向上的变化规律为：B＝B0＋kx，并且x≥0．现在导体棒中点施加一垂直于棒的水平拉力F，使导体棒由静止开始向右做匀加速直线运动，加速度大小为a．设导体棒的质量为m，两导轨间距为L．不计导体棒与导轨间的摩擦，导体棒与导轨接触良好，不计其余部分的电阻．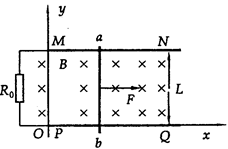
（1）请通过分析推导出水平拉力F的大小随横坐标x变化的关系式；
（2）如果已知导体棒从x＝0运动到x＝x0的过程中，力F做的功为W，求此过程回路中产生的焦耳热Q；
（3）若B0＝0．1T，k＝0．2T／m，R0＝0．1Ω，r＝0．1Ω／m，L＝0．5m，
a＝4m／s2，求导体棒从x＝0运动到x＝1m的过程中，通过电阻R0的电荷量q．
（18分）如图所示，水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0，不计电阻的导体棒ab静置在导轨的左端MP处，并与MN垂直．以导轨PQ的左端为坐标原点O，建立直角坐标系xOy，Ox轴沿PQ方向．每根导轨单位长度的电阻为r．垂直于导轨平面的非匀强磁场磁感应强度在y轴方向不变，在x轴方向上的变化规律为：B＝B0＋kx，并且x≥0．现在导体棒中点施加一垂直于棒的水平拉力F，使导体棒由静止开始向右做匀加速直线运动，加速度大小为a．设导体棒的质量为m，两导轨间距为L．不计导体棒与导轨间的摩擦，导体棒与导轨接触良好，不计其余部分的电阻．
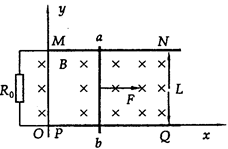
（1）请通过分析推导出水平拉力F的大小随横坐标x变化的关系式；
（2）如果已知导体棒从x＝0运动到x＝x0的过程中，力F做的功为W，求此过程回路中产生的焦耳热Q；
（3）若B0＝0．1T，k＝0．2T／m，R0＝0．1Ω，r＝0．1Ω／m，L＝0．5m，
a＝4m／s2，求导体棒从x＝0运动到x＝1m的过程中，通过电阻R0的电荷量q．
（1）请通过分析推导出水平拉力F的大小随横坐标x变化的关系式；
（2）如果已知导体棒从x＝0运动到x＝x0的过程中，力F做的功为W，求此过程回路中产生的焦耳热Q；
（3）若B0＝0．1T，k＝0．2T／m，R0＝0．1Ω，r＝0．1Ω／m，L＝0．5m，
a＝4m／s2，求导体棒从x＝0运动到x＝1m的过程中，通过电阻R0的电荷量q．