题目内容
(18分)如图所示,水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0,不计电阻的导体棒ab静置在导轨的左端MP处,并与MN垂直.以导轨PQ的左端为坐标原点O,建立直角坐标系xOy,Ox轴沿PQ方向.每根导轨单位长度的电阻为r.垂直于导轨平面的非匀强磁场磁感应强度在y轴方向不变,在x轴方向上的变化规律为:B=B0+kx,并且x≥0.现在导体棒中点施加一垂直于棒的水平拉力F,使导体棒由静止开始向右做匀加速直线运动,加速度大小为a.设导体棒的质量为m,两导轨间距为L.不计导体棒与导轨间的摩擦,导体棒与导轨接触良好,不计其余部分的电阻.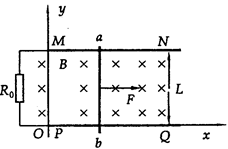
(1)请通过分析推导出水平拉力F的大小随横坐标x变化的关系式;
(2)如果已知导体棒从x=0运动到x=x0的过程中,力F做的功为W,求此过程回路中产生的焦耳热Q;
(3)若B0=0.1T,k=0.2T/m,R0=0.1Ω,r=0.1Ω/m,L=0.5m,
a=4m/s2,求导体棒从x=0运动到x=1m的过程中,通过电阻R0的电荷量q.
(1) 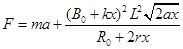 (2) W-max0 ; (3) 0.5C
(2) W-max0 ; (3) 0.5C
解析试题分析:(1)设导体棒运动到坐标为x处的速度为v,根据法拉第电磁感应定律可得:E=BLv①
由欧姆定律: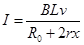 ②
②
由于棒做匀加速运动,所以有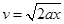 ③
③
此时棒受到的安培力: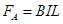 ④
④
由牛顿第二定律: ⑤
⑤
联立①②③④⑤可得: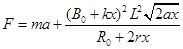
(2)设导体棒在x=x0处的动能为EK,则由动能定理可得:EK=max0 ⑥
由能量守恒定律可知:W=Q+EK ⑦
将⑥式代入⑦式可解得:Q=W-max0
(3)由①②两式可得: ⑧
⑧
因为a=vt,将题中所给的数据代入⑧式可得:I="2t(A)" ⑨
可知回路中的电流与时间成正比,所以在0-t时间内,通过R0的电荷量为:
由匀加速直线运动的规律可得: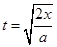 ,当x=x0时,有
,当x=x0时,有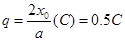
考点:法拉第电磁感应定律及能量守恒定律;牛顿第二定律的应用。

 一线名师权威作业本系列答案
一线名师权威作业本系列答案

 。圆形轨道是光滑的,水平轨道足够长。取重力加速度g=10m/s2。求:
。圆形轨道是光滑的,水平轨道足够长。取重力加速度g=10m/s2。求: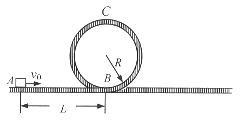
 ;
;
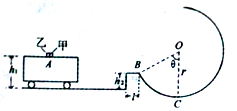

 m,今以O点为原点建立平面直角坐标系。现用F=5N的水平恒力拉动小物块,已知重力加速度
m,今以O点为原点建立平面直角坐标系。现用F=5N的水平恒力拉动小物块,已知重力加速度 .
.