网址:http://m.1010jiajiao.com/timu_id_10827[举报]
一、选择题:本题考查基本知识和基本运算。每小题5分,满分50分。
(1)A (2)C (3)A (4)B (5)C (6)C
(7)A (8)D (9)B (10)D
二、填空题:本题考查基本知识和基本运算。每小题4分,满分16分。
(11)-1 (12) (13)4 (14)
(1) 设集合≤x≤2},B={x|0≤x≤4},则A∩B=A
(A)[0,2] (B)[1,2] (C)[0,4] (D)[1,4]
【考点分析】本题考查集合的运算,基础题。
解析:,故选择A。
【名师点拔】集合是一个重要的数学语言,注意数形结合。
(2) 已知C
(A) (B) (C) (D)
【考点分析】本题考查复数的运算及性质,基础题。
解析:,由、是实数,得
∴,故选择C。
【名师点拔】一个复数为实数的充要条件是虚部为0。
(3)已知,则A
(A)1<n<m (B) 1<m<n (C)m<n<1 (D) n<m<1
【考点分析】本题考查对数函数的性质,基础题。
解析:由知函数为减函数,由得
,故选择A。
(4)在平面直角坐标系中,不等式组表示的平面区域的面积是B
【考点分析】本题考查简单的线性规划的可行域、三角形的面积。
解析:由题知可行域为,
,故选择B。
【名师点拔】
(5)若双曲线上的点到左准线的距离是到左焦点距离的,则C
(A) (B) (C) (D)
【考点分析】本题考查双曲线的第二定义,基础题。
解析:由题离心率,由双曲线的第二定义知
,故选择C。
【名师点拔】本题在条件中有意识的将双曲线第二定义“到左焦点距离与到左准线的距离是定值”中比的前后项颠倒为“到左准线的距离是到左焦点距离的”,如本题改为填空题,没有了选择支的提示,则难度加大。
(6)函数的值域是C
(A)[-,] (B)[-,] (C)[] (D)[]
【考点分析】本题考查三角函数的性质,基础题。
解析:,故选择C。
【名师点拔】本题是求有关三角函数的值域的一种通法,即将函数化为
或的模式。
(7)“”是“”的A
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
【考点分析】本题考查平方不等式和充要条件,基础题。
解析:由能推出;但反之不然,因此平方不等式的条件是。
【名师点拔】
(8)若多项式D
(A)9 (B)10 (C)-9 (D)-10
【考点分析】本题考查二项式展开式的特殊值法,基础题。
解析:令,得,
令,得
(9)如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是B
【考点分析】本题考查球面距的计算,基础题。
解析:如图,
∴
∴,∴点E、F在该球面上的球面距离为
故选择B。
【名师点拔】两点球面距的计算是立体几何的一个难点,其通法的关键是求出两点的球面角,而求球面角又需用余弦定理。
(10)函数满足,则这样的函数个数共有D
(A)1个 (B)4个 (C)8个 (D)10个
【考点分析】本题考查抽象函数的定义,中档题。
解析:即
(11)设为等差数列的前项和,若,则公差为 -1 (用数字作答)。
【考点分析】本题考查等差数列的前项和,基础题。
解析:设首项为,公差为,由题得
【名师点拔】数学问题解决的本质是,你已知什么?从已知出发又能得出什么?完成了这些,也许水到渠成了。本题非常基础,等差数列的前项和公式的运用自然而然的就得出结论。
(12)对,记函数的最小值是 .
【考点分析】本题考查新定义函数的理解、解绝对值不等式,中档题。
,其图象如右,
则。
【名师点拔】数学中考查创新思维,要求必须要有良好的数学素养。
(13)设向量满足 b,若,则的值是 4 。
【考点分析】本题考查向量的代数运算,基础题。
解析:
【名师点拔】向量的模转化为向量的平方,这是一个重要的向量解决思想。
(14)正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .
三、解答题
(15)本题主要考查三角函数的图像,已知三角函数求角,向量夹角的计算等基础知识和基本的运算能力。满分14分。
解:(I)因为函数图像过点,
所以即
因为,所以.
(II)由函数及其图像,得
所以从而
,
故.
(16)本题主要考查二次函数的基本性质与不等式的应用等基础知识。满分14分。
证明:(I)因为,
所以.
由条件,消去,得
;
由条件,消去,得
,.
故.
(II)抛物线的顶点坐标为,
在的两边乘以,得
.
又因为
而
所以方程在区间与内分别有一实根。
故方程在内有两个实根.
(17)本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。满分14分。
解:方法一:
(I)因为是的中点,,
所以.
因为平面,所以
,
从而平面.
因为平面,
所以.
(II)取的中点,连结、,
则,
所以与平面所成的角和与平面所成的角相等.
因为平面,
所以是与平面所成的角.
在中,
.
故与平面所成的角是.
方法二:
如图,以为坐标原点建立空间直角坐标系,设,则
.
(I) 因为
,
所以
(II) 因为
,
所以,
又因为,
所以平面
因此的余角即是与平面所成的角.
因为
,
所以与平面所成的角为.
(18)本题主要考察排列组合、概率等基本知识,同时考察逻辑思维能力和数学应用能力。满分14分。
解:(I)记“取到的4个球全是红球”为事件.
(II)记“取到的4个球至多有1个红球”为事件,“取到的4个球只有1个红球”为事件,“取到的4个球全是白球”为事件.
由题意,得
所以
,
化简,得
解得,或(舍去),
故 .
(19)本题主要考查直线与椭圆的位置关系、椭圆的几何性质,同时考察解析几何的基本思想方法和综合解题能力。满分14分。
解:(I)过点、的直线方程为
因为由题意得 有惟一解,
即有惟一解,
所以
(),
故
又因为 即
所以
从而得
故所求的椭圆方程为
(II)由(I)得
故
从而
由
解得
所以
因为
又得
因此
(20)本题主要考查函数的导数、数列、不等式等基础知识,以及不等式的证明,同时考查逻辑推理能力。满分14分。
证明:(I)因为
所以曲线在处的切线斜率
因为过和两点的直线斜率是
所以.
(II)因为函数当时单调递增,
而
,
所以,即
因此
又因为
令
则
因为
所以
因此
故
(本小题共13分)若有穷数列{an}满足:(1)首项a1=1,末项am=k,(2)an+1= an+1或an+1=2an ,(n=1,2,…,m-1),则称数列{an}为k的m阶数列.
(Ⅰ)请写出一个10的6阶数列;
(Ⅱ)设数列{bn}是各项为自然数的递增数列,若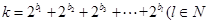 ,且
,且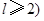 ,求m的最小值.
,求m的最小值.
(考生务必将答案答在答题卡上,在试卷上作答无效)
查看习题详情和答案>>
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵
|
C.(选修4-4:坐标系与参数方程)
已知曲线C1:
|
| π |
| 4 |
| 2 |
(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<
| c |
| 4 |
| c |
| 6 |
B.选修4-2:矩阵与变换
已知矩阵A=
|
| β |
|
| α |
| α |
| β |
C.选修4-4:极坐标与参数方程
在直角坐标系x0y中,直线l的参数方程为
|
| π |
| 4 |
(1)求直线l的倾斜角;
(2)若直线l与曲线l交于A、B两点,求AB.
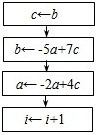
 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,
|
(1)可考虑利用算法来求am,bm的值,其中m为给定的数据(m≥2,m∈N).右图算法中,虚线框中所缺的流程,可以为下面A、B、C、D中的
(请填出全部答案)
A、
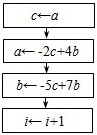 B、
B、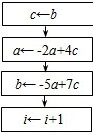
C、
 D、
D、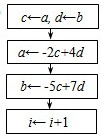
(2)我们可证明当a≠b,5a≠4b时,{an-bn}及{5an-4bn}均为等比数列,请按答纸题要求,完成一个问题证明,并填空.
证明:{an-bn}是等比数列,过程如下:an-bn=(-2an-1+4bn-1)+(5an-1-7bn-1)=3an-1-3bn-1=3(an-1-bn-1)
所以{an-bn}是以a1-b1=a-b≠0为首项,以
同理{5an-4bn}是以5a1-4b1=5a-4b≠0为首项,以
(3)若将an,bn写成列向量形式,则存在矩阵A,使
|
|
|
|
|
①写出矩阵A=
|
|
|
|
|
|
计算过程如下: