网址:http://m.1010jiajiao.com/timu_id_10729[举报]
一、
1.C 2.D 3.B 4.C 5.B 6.D 7.D 8.C 9.C 10.B 11.C 12.A
二、13. 14. 15. 16.72
三、
17.(I)证明:取BD中点M,连结MC,FM,
∵F为BD1中点, ∴FM∥D1D且FM=D1D
又EC=CC1,且EC⊥MC,
∴四边形EFMC是矩形 ∴EF⊥CC1
又CM⊥面DBD1 ∴EF⊥面DBD1
∵BD1面DBD1,
∴EF⊥BD1 故EF为BD1与CC1的公垂线
(II)解:连结ED1,有V
由(I)知EF⊥面DBD1,设点D1到面BDE的距离为d,
则S△DBC?d=S△DCD?EF.
∵AA1=2?AB=1.
故点D1到平面BDE的距离为.
18.解:设z=
由题设
即
(舍去)
即|z|=
19.(I)解∵
(II)证明:由已知
=
所以
20.解(I)
所以函数的最小正周期为π,最大值为.
(Ⅱ)由(Ⅰ)知
1
1
1
21.解:如图建立坐标系:以O为原点,正东方向为x轴正向.
在时刻:t(h)台风中心的坐标为
此时台风侵袭的区域是,
其中t+60,
若在t时,该城市O受到台风的侵袭,则有
即
即, 解得.
答:12小时后该城市开始受到台风气侵袭
22.解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得
点P到定点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)
设,
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:, ①
直线GE的方程为:. ②
从①,②消去参数k,得点P(x,y)坐标满足方程,
整理得.
当时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当时,点P到椭圆两个焦点的距离之和为定值.
当时,点P到椭圆两个焦点的距离之
和为定值.
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
查看习题详情和答案>>
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2”拓展到空间,类比平面几何的勾股定理,“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则可得”猜想正确的是( )
A.AB2+AC2+
AD2=BC2 +CD2 +BD2
B.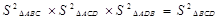
C. D.AB2×AC2×AD2=BC2
×CD2 ×BD2
D.AB2×AC2×AD2=BC2
×CD2 ×BD2
查看习题详情和答案>>
 ”拓展到空间,类比平面几何的勾股定理,“设三棱锥A—BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( )
”拓展到空间,类比平面几何的勾股定理,“设三棱锥A—BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( )


