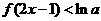20. 解(Ⅰ)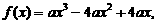
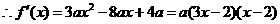 令
令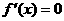 ,得
,得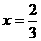 或2.
或2.
∵函数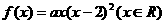 有极大值32,
有极大值32,
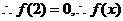 在
在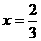 时取得极大值.
时取得极大值. 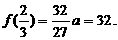 解得
解得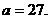
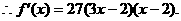
当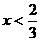 时,
时,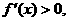 当
当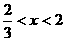 时,
时,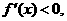
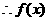 在
在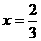 时,有极大值32.
时,有极大值32. 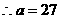 时函数
时函数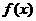 有极大值32. ……7分
有极大值32. ……7分
(Ⅱ)由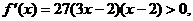 得
得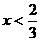 或
或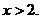
∴函数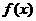 的单调增区间是(-
的单调增区间是(-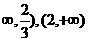 ;单调减区间是(
;单调减区间是(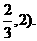
1. 台州二模
(20)(本题满分 分)
分)
数列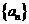 中,
中,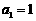 ,当
,当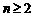 时,其前
时,其前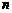 项的和
项的和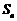 满足
满足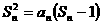 .
.
(Ⅰ)证明:数列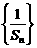 是等差数列;
是等差数列;
(Ⅱ)设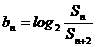 ,数列
,数列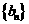 的前
的前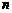 项和为
项和为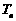 ,求满足
,求满足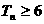 的最小正整数
的最小正整数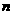 .
.
(20)解(Ⅰ)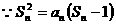
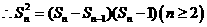
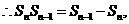 即
即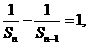
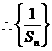 是1为首项,1为公差的等差数列. ………………………………7分
是1为首项,1为公差的等差数列. ………………………………7分
(Ⅱ)由(Ⅰ)知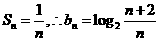 ,
,
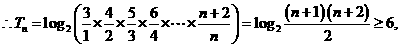
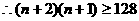
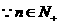
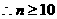 ,
,
所以满足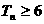 的最小正整数为10. ………………………………14分
的最小正整数为10. ………………………………14分
(21)(本题满分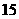 分)
分)
已知函数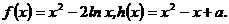
(Ⅰ)求函数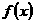 的极值;
的极值;
(Ⅱ)设函数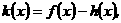 若函数
若函数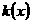 在
在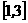 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 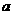 的取值范围.
的取值范围.
(21)解: (Ⅰ)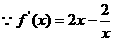 ,令
,令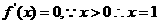
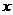 |
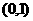 |
1 |
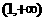 |
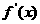 |
_ |
0 |
+ |
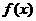 |
减 |
1 |
增 |
所以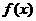 的极小值为1,无极大值.
……………………………………7分
的极小值为1,无极大值.
……………………………………7分
(Ⅱ)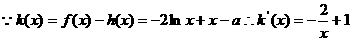 ,若
,若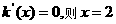
当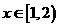 时,
时,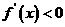 ;当
;当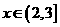 时,
时,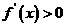 .
.
故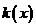 在
在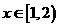 上递减,在
上递减,在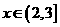 上递增. ……………………………10分
上递增. ……………………………10分
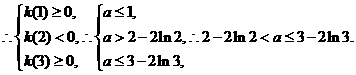
所以实数 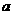 的取值范围是
的取值范围是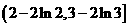 ………………………………15分
………………………………15分
(22)(本题满分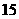 分)已知曲线
分)已知曲线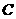 上的动点
上的动点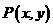 满足到点
满足到点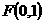 的距离比到直线
的距离比到直线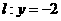 的距离小
的距离小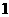 .
.
(Ⅰ)求曲线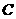 的方程;
的方程;
(Ⅱ)动点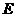 在直线
在直线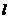 上,过点
上,过点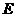 分别作曲线
分别作曲线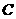 的切线
的切线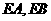 ,切点为
,切点为 、
、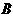 .
.
(ⅰ)求证:直线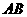 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线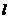 上是否存在一点
上是否存在一点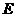 ,使得
,使得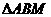 为等边三角形(
为等边三角形(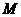 点也在直线
点也在直线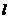 上)?若存在,求出点
上)?若存在,求出点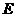 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
(22)解:(Ⅰ) 曲线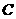 的方程
的方程 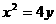 …………………………………………5分
…………………………………………5分
(Ⅱ)(ⅰ)设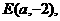
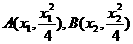 ,
,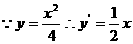
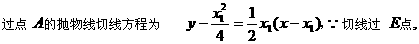
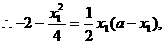 整理得:
整理得: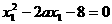
同理可得: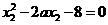
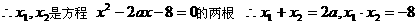
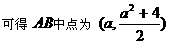
又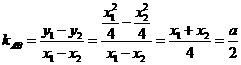

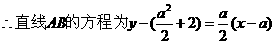
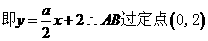 ………………………………10分
………………………………10分
(ⅱ)由(ⅰ)知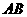 中点
中点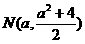 ,
,
当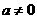 时,则
时,则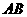 的中垂线方程为
的中垂线方程为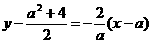
 的中垂线与直线
的中垂线与直线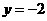 的交点
的交点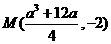
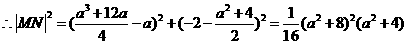
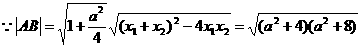
若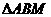 为等边三角形,则
为等边三角形,则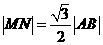
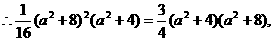
解得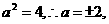 此时
此时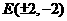 ,
,
当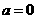 时,经检验不存在满足条件的点
时,经检验不存在满足条件的点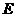
综上可得:满足条件的点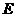 存在,坐标为
存在,坐标为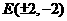 . ……………………15分
. ……………………15分
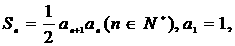
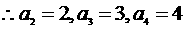 …………… 4分
…………… 4分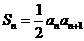 , 故
, 故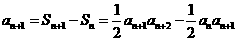
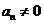 , 当然
, 当然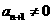 , 所以
, 所以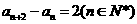 .
.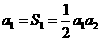 , 且
, 且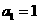 , 故
, 故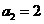 .
.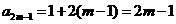 ,
, 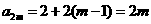 ,
,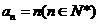 .……………………………………8分
.……………………………………8分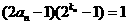 , 得
, 得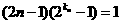 ,
, 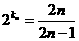
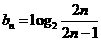 .
.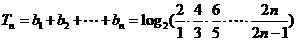 .
.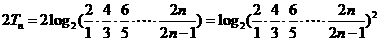 .
.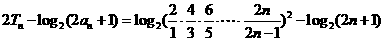
 .
.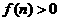 , 所以
, 所以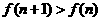 .
.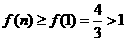 , 从而
, 从而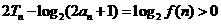 .
.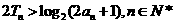 .……………………………………14分
.……………………………………14分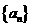 的前
的前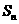 ,且
,且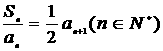 ,其中
,其中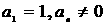 , (1)求
, (1)求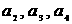 ,并猜想数列
,并猜想数列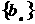 满足
满足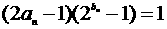 ,
,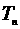 为
为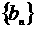 的前
的前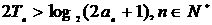 ;
;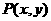 为曲线
为曲线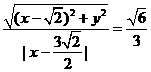 (2分)
(2分)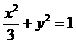 ,
,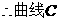 为椭圆,其方程为
为椭圆,其方程为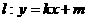 ,
, 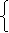 由
由 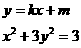 消去
消去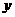 得:
得: 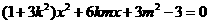 (6分)
(6分)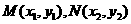 ,
,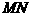 中点
中点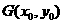 ,
,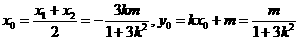 ,
,
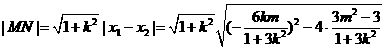
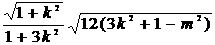 ………(
1)
………(
1)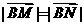 ,
,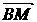 与
与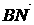 夹角为
夹角为 ,
,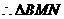 为等边三角形,
为等边三角形,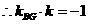 ,即
,即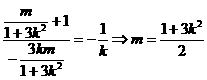 ,………(2)
,………(2) 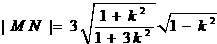 ,
,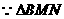 为等边三角形,
为等边三角形,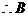 到
到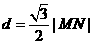 ,
,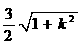
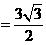
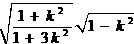 解得:
解得: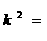
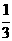 ,
,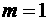 ,
,
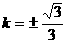 ,
,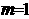 使方程有解,所以直线
使方程有解,所以直线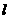 的方程为:
的方程为: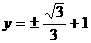 (12分)
(12分)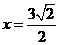 的距离与它到点
的距离与它到点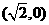 的距离之比是
的距离之比是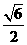 。 (I)求曲线
。 (I)求曲线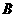 为曲线
为曲线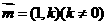 的直线
的直线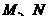 两点,使
两点,使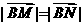 ,且
,且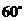 ?若存在,求出
?若存在,求出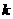 值,并写出直线
值,并写出直线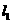 、
、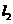 之间的B处有一重点文化古迹,该古迹到直道
之间的B处有一重点文化古迹,该古迹到直道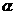 ,直道
,直道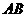 所在直线的夹角为
所在直线的夹角为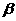 ,
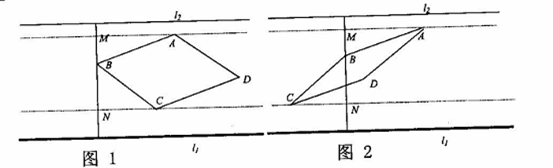
,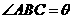 。
。
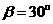 ,求
,求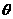 。
。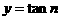 ,试探求
,试探求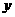 一关于
一关于



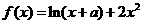 。
。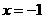 时,
时,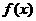 取得极值,求
取得极值,求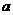 的值;
的值;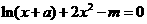 恰好有三个零点,求
恰好有三个零点,求 的取值范围;
的取值范围;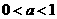 时,解不等式
时,解不等式