20.(本小题满分13分)设M是由满足下列条件的函数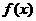 构成的集合:“①方程
构成的集合:“①方程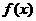
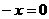 有实数根;②
有实数根;②
函数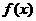 的导数
的导数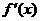 满足
满足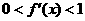 .”
.”
(I)判断函数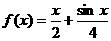 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素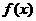 具有下面的性质:若
具有下面的性质:若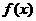 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n] D,都存在
D,都存在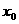
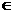 [m,n],使得等式
[m,n],使得等式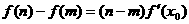 成立”,
成立”,
试用这一性质证明:方程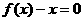 只有一个实数根;
只有一个实数根;
(III)设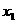 是方程
是方程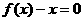 的实数根,求证:对于
的实数根,求证:对于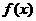 定义域中任意的
定义域中任意的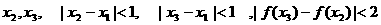 .
.
21(本小题满分14分)在直角坐标系中,O为坐标原点,F是x轴正半轴上的一点,若△OFQ的面积为S,且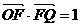 .
.
(Ⅰ)(本问4分)若 夹角θ的取值范围;
夹角θ的取值范围;
(Ⅱ)(本问5分)设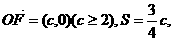 若以O为中心,F为焦点的椭圆经过点Q,求|
若以O为中心,F为焦点的椭圆经过点Q,求|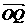 |的最小值以及此时的椭圆方程;
|的最小值以及此时的椭圆方程;
|
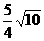 的弦AB的两个端点在椭圆E上滑动,M为线段AB的中点,求M点到椭圆右准线距离的最大值及对应的AB直线的方程.
的弦AB的两个端点在椭圆E上滑动,M为线段AB的中点,求M点到椭圆右准线距离的最大值及对应的AB直线的方程.
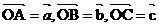 ,又OA、BC的中点分别为D、E,则向量
,又OA、BC的中点分别为D、E,则向量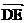 等于(
)
等于(
)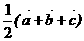 B
B 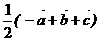 C
C 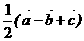 D
D 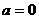 是直线
是直线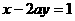 和
和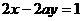 平行的(
)
平行的(
)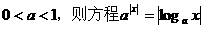 的实根个数是
( )
的实根个数是
( )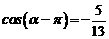 ,且
,且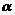 是第四象限的角,则
是第四象限的角,则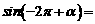 ( )
( )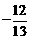 B
B
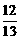 C
C 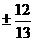 D
D
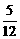
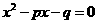 的解集为A,方程
的解集为A,方程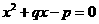 的解集为B,若
的解集为B,若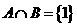 ,
,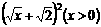 ,设正项数列{an}的首项a1=2,前n 项和Sn满足Sn=f(Sn-1)(n>1,且n∈N*);
,设正项数列{an}的首项a1=2,前n 项和Sn满足Sn=f(Sn-1)(n>1,且n∈N*);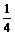
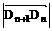 -1,若Cn=
-1,若Cn=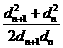 ,求证:C1+C2+C3+…+Cn <n+1.
,求证:C1+C2+C3+…+Cn <n+1.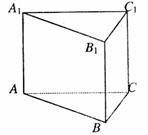 (Ⅰ)若α在区间
(Ⅰ)若α在区间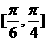 上变化,求x的变化范围;
上变化,求x的变化范围;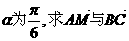 所成的角.
所成的角.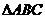 内接于以O为圆心,1为半径的圆,且
内接于以O为圆心,1为半径的圆,且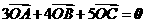 .
.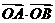 ,
,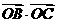 ,
,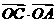 ;(2)求
;(2)求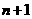 个球(其中
个球(其中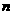 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出 个球
个球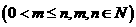 ,共有
,共有 种取法。在这
种取法。在这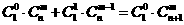 ,即有等式:
,即有等式: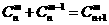 成立。试根据上述思想化简下列式子:
成立。试根据上述思想化简下列式子: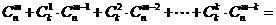 。
。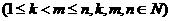 。
。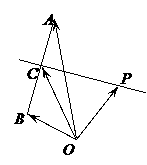 15如图,
15如图,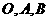 是平面上的三点,向量
是平面上的三点,向量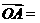 a,
a, 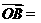 b,
b,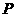 为线段
为线段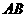 的垂直平分线
的垂直平分线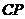 上任意一点,向量
上任意一点,向量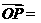 p若|a|=m,|b|=n,则p(a
p若|a|=m,|b|=n,则p(a 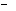 b)等于
b)等于