0 50558 50566 50572 50576 50582 50584 50588 50594 50596 50602 50608 50612 50614 50618 50624 50626 50632 50636 50638 50642 50644 50648 50650 50652 50653 50654 50656 50657 50658 50660 50662 50666 50668 50672 50674 50678 50684 50686 50692 50696 50698 50702 50708 50714 50716 50722 50726 50728 50734 50738 50744 50752 447348
 的首项为1,前10项的和为145,求
的首项为1,前10项的和为145,求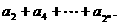
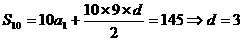
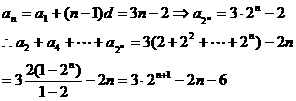
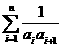 。
。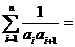
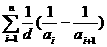
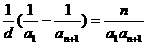
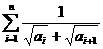 也可用裂项求和法。
也可用裂项求和法。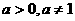 ,数列
,数列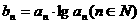 ,求数列
,求数列 的前
的前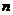 项和
项和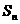 。
。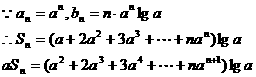
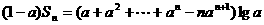
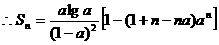 。
。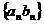
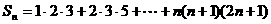 。
。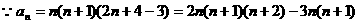
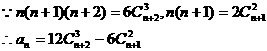
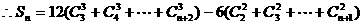
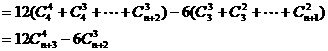
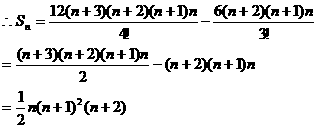
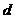 ,且首项为
,且首项为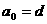 的等差数列,求和:
的等差数列,求和: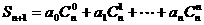
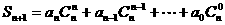
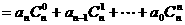
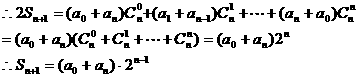
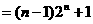 ,是否存在等差数列
,是否存在等差数列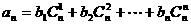 对一切自然数n都成立。
对一切自然数n都成立。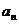 满足:
满足: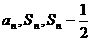
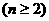 成
成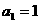 ,求数列
,求数列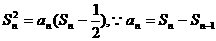
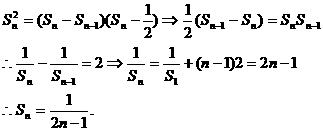
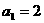 ,
,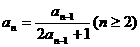 ,
,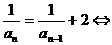
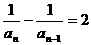
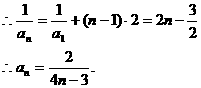
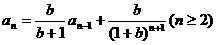 可转化为
可转化为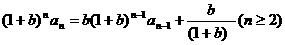
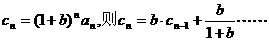 ①
①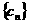 中,
中,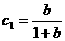 ,
,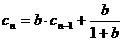 ,
,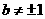 。求出用n和b表示的an的关系式。
。求出用n和b表示的an的关系式。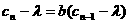 的形式。
的形式。
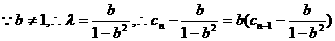

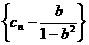 是首项为
是首项为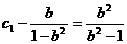 ,公比为
,公比为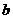 的
的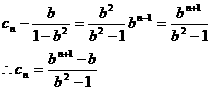
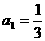 ,前
,前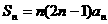 ,试求通项公式
,试求通项公式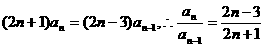
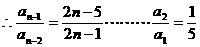
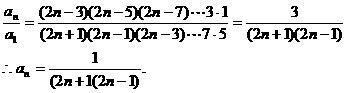
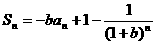 ,其中b是与n无关的常数,且
,其中b是与n无关的常数,且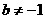 。
。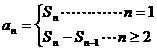 得:
得: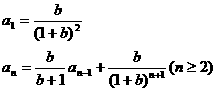
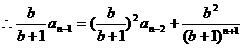
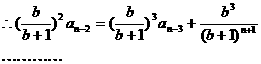
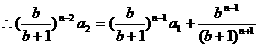
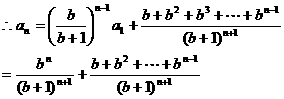
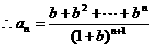
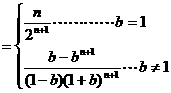
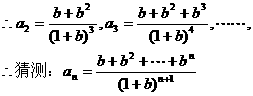
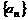 的首项为a1=1,前n项和Sn满足关系
的首项为a1=1,前n项和Sn满足关系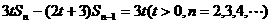
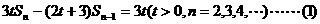
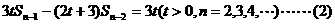
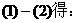
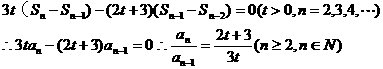 所以,数列
所以,数列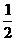 )的值;
)的值;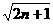 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.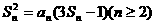
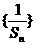 为等差数列
为等差数列