摘要:数列的求和 等差数列与等比数列的有限项求和总是有公式可求的.其它的数列的求和不总是可求的.但某些特殊数列的求和可采用分部求和法转化为等差数列或等比数列的和或用裂项求和法.错位相减法.逆序相加法.组合化归法.递推法. ① 分部求和法 例1. 已知等差数列的首项为1.前10项的和为145.求 解析:首先由 则: ② 裂项求和法 例2. 已知数列为等差数列.且公差不为0.首项也不为0. 求和:. 解析:首先考虑 则= 点评:已知数列为等差数列.且公差不为0.首项也不为0.下列求和 也可用裂项求和法. ③ 错位相减法 例3.已知.数列是首项为a.公比也为a的等比数列.令 .求数列的前项和. 解析: ①-②得: . 点评:设数列的等比数列.数列是等差数列.则数列 的前项和求解.均可用错位相减法. ④ 组合化归法 例4.求和: . 解析: 而连续自然数可表示为组合数的形式.于是.数列的求和便转化为组合数的 求和问题了. 点评:可转化为连续自然数乘积的数列求和问题.均可考虑组合化归法. ⑤ 逆序相加法 例5.设数列是公差为.且首项为的等差数列.求和: 解析:因为 点评:此类问题还可变换为探索题形: 已知数列的前项和.是否存在等差数列使得 对一切自然数n都成立. ⑥ 递推法 例6. 已知数列的前项和与满足:成 等比数列.且.求数列的前项和. 解析:由题意: 点评:本题的常规方法是先求通项公式.然后求和.但逆向思维.直接求出数列的前项和的递推公式.是一种最佳解法.
网址:http://m.1010jiajiao.com/timu3_id_506560[举报]
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义.
(2)探索等和数列{an}的奇数项与偶数项各有什么特点,并加以说明.
(3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.?
查看习题详情和答案>>
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义.
(2)探索等和数列{an}的奇数项与偶数项各有什么特点,并加以说明.
(3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.?
查看习题详情和答案>>已知等差数列{an}的首项为4,公差为4,其前n项和为Sn,则数列 {![]() }的前n项和为( )
}的前n项和为( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考点: | 数列的求和;等差数列的性质. |
| 专题: | 等差数列与等比数列. |
| 分析: | 利用等差数列的前n项和即可得出Sn,再利用“裂项求和”即可得出数列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴数列 { 故选A. |
| 点评: | 熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键. |
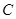 :
: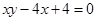 ,数列
,数列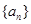 的首项
的首项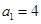 ,且当
,且当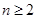 时,点
时,点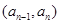 恒在曲线
恒在曲线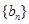 满足
满足 。
。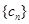 满足
满足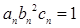 ,试比较数列
,试比较数列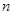 项和
项和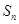 与2的大小。
与2的大小。 中,若
中,若 ,则
,则 是
是 是等方差数列;③若
是等方差数列;③若