23. 启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量是10万件。为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的啊销售量将是原销售量的y倍,且y=-1/10X2+7/10X+7/10,如果把利润看作是销售总额减去成本费和广告费:
启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量是10万件。为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的啊销售量将是原销售量的y倍,且y=-1/10X2+7/10X+7/10,如果把利润看作是销售总额减去成本费和广告费:
(1) 试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少元时,公司获得的年利润最大,最大年利润是多少万元;
(2) 把(1)中的最大利润留出3万元作广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资额和预计年收益如下表:
|
项目 |
A |
B |
C |
D |
E |
F |
|
每股(万元) |
5 |
2 |
6 |
4 |
6 |
8 |
|
收益(万元) |
0.55 |
0.4 |
0.6 |
0.5 |
0.9 |
1 |
如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元,问有几种符合要求的投资方式?写出每种投资方式所选的项目。
20.某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价X元与销售量Y件之间有如下关系:
|
X |
3 |
5 |
9 |
11 |
|
Y |
18 |
14 |
6 |
2 |
(1) 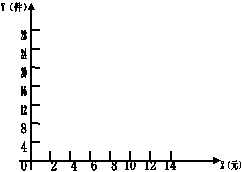 在所给的直角坐标系中,根据表中提供的数据描出实数对(X,Y)对应点;猜测并确定日销售量Y(件)与日销售单价X元之间的函数关系式,并画出图象。
在所给的直角坐标系中,根据表中提供的数据描出实数对(X,Y)对应点;猜测并确定日销售量Y(件)与日销售单价X元之间的函数关系式,并画出图象。
(3) 设经营此商品的日销售利润(不考虑其它因素)为P元,根据日销售规律:
① 试求日销售利润P(元)与销售单价X(元)之间的数关系式,并求出日销售单价X为多少时,才能获得最大日销售利润,试问日销售利润P是否存在最小值?若有,试求出,若无,说明理由;
② 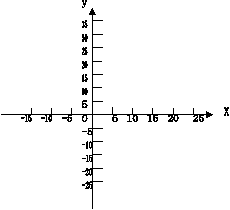 在坐标系内画出日销售利润P元与日销售单价X元之间的函数据关系图象的简图,观察图象,写出X与P的取值范围。
在坐标系内画出日销售利润P元与日销售单价X元之间的函数据关系图象的简图,观察图象,写出X与P的取值范围。
19.某公司生产一种产品每年投入固定成本0.5万元,此外,每生产100件这种产品还需要增加投资0.25万元。
|
T(百万) |
0 |
1 |
2 |
··· |
|
Q(万元) |
0 |
4.5 |
8 |
··· |
经预测知,市场对这种产品的年需求量为500件,而且出售的这种产品的数量为T(单位:百件)时,销售所得的收入Q是T的二次函数,它们的关系如下表:(Q的单位为:万元)
(1) 求出Q与T的函数关系式。
(2) 若把该公司这种产品的年产量设为X(单位:百件,X >0)。试把该公司生产并销售这种产品所得的年利润Y表示为当年产量X函数。(Y的单位为:万元),并画出图象;
(3) 当该公司的年产量多少时,当年所得利润最大?年总产量多大时,当年不会亏本?(注: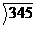 =18.57)
=18.57)
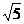 +1)(
+1)(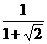 +
+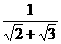 +
+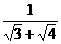 +…+
+…+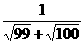 ).
).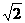 时,求
时,求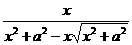 +
+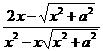 +
+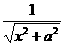 的值.
的值.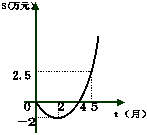 求截止到几个月末公司累积利润可达到30万元;
求截止到几个月末公司累积利润可达到30万元;