0 159950 159958 159964 159968 159974 159976 159980 159986 159988 159994 160000 160004 160006 160010 160016 160018 160024 160028 160030 160034 160036 160040 160042 160044 160045 160046 160048 160049 160050 160052 160054 160058 160060 160064 160066 160070 160076 160078 160084 160088 160090 160094 160100 160106 160108 160114 160118 160120 160126 160130 160136 160144 447348
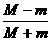 v0
v0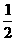 mv′2-
mv′2-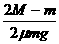 v02
v02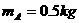 ,
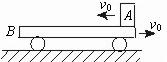
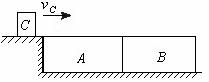
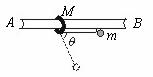
,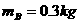 ,它们的下底面光滑,上表面粗糙;另有一质量
,它们的下底面光滑,上表面粗糙;另有一质量 的滑块C(可视为质点),以
的滑块C(可视为质点),以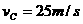 的速度恰好水平地滑到A的上表面,如图所示,由于摩擦,滑块最后停在木块B上,B和C的共同速度为3.0m/s,求:
的速度恰好水平地滑到A的上表面,如图所示,由于摩擦,滑块最后停在木块B上,B和C的共同速度为3.0m/s,求: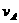 ; (2)滑块C离开A时的速度
; (2)滑块C离开A时的速度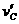 。
。
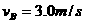 运动,由动量守恒定律有
运动,由动量守恒定律有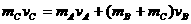
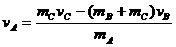
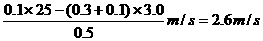
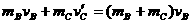
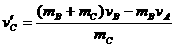
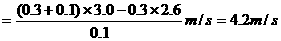
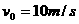 ;m1=0.3kg的大块速度为
;m1=0.3kg的大块速度为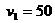 m/s、m2=0.2kg的小块速度为
m/s、m2=0.2kg的小块速度为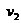 ,方向不清,暂设为正方向。
,方向不清,暂设为正方向。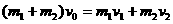
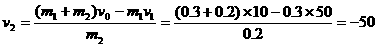 m/s
m/s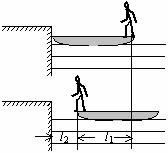
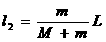
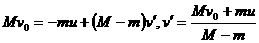
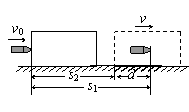 解析:子弹和木块最后共同运动,相当于完全非弹性碰撞。
解析:子弹和木块最后共同运动,相当于完全非弹性碰撞。
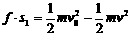 ……①
……①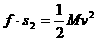 ……②
……②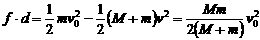 ……③
……③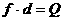 ,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。
,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。 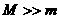 ,则s2<<d。木块的位移很小。但这种运动物体与静止物体相互作用,最后共同运动的类型,全过程动能的损失量均可用公式:
,则s2<<d。木块的位移很小。但这种运动物体与静止物体相互作用,最后共同运动的类型,全过程动能的损失量均可用公式: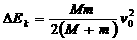 …④
…④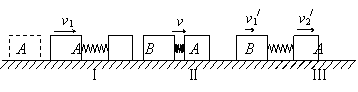 两个物体作用时间极短,满足内力远大于外力,可以认为动量守恒。
两个物体作用时间极短,满足内力远大于外力,可以认为动量守恒。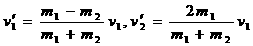 。(这个结论最好背下来,以后经常要用到。)
。(这个结论最好背下来,以后经常要用到。)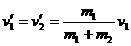 。在完全非弹性碰撞过程中,系统的动能损失最大,为:
。在完全非弹性碰撞过程中,系统的动能损失最大,为: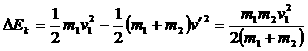 。
。 [例1] 质量为M的楔形物块上有圆弧轨道,静止在水平面上。质量为m的小球以速度v1向物块运动。不计一切摩擦,圆弧小于90°且足够长。求小球能上升到的最大高度H 和物块的最终速度v。
[例1] 质量为M的楔形物块上有圆弧轨道,静止在水平面上。质量为m的小球以速度v1向物块运动。不计一切摩擦,圆弧小于90°且足够长。求小球能上升到的最大高度H 和物块的最终速度v。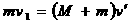
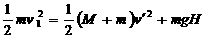 解得
解得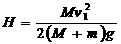
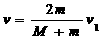
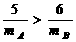 ;碰后A的速度不大于B的速度,
;碰后A的速度不大于B的速度,  ;又因为碰撞过程系统动能不会增加,
;又因为碰撞过程系统动能不会增加,
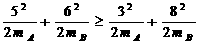 ,由以上不等式组解得:
,由以上不等式组解得: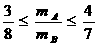
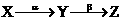 ,
,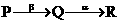 ,下列说法正确的是
,下列说法正确的是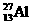 后,变为磷(P)的同位素,同时放出一个中子,其核反应方程式是_________,随后磷的同位素又发生衰变,变成另一元素硅(Si),并放出一个正电子,其反应方程式是____________.
后,变为磷(P)的同位素,同时放出一个中子,其核反应方程式是_________,随后磷的同位素又发生衰变,变成另一元素硅(Si),并放出一个正电子,其反应方程式是____________.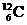 和
和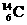 ,它们具有相同的____数和不同的____数,这样的原子互称为____。
,它们具有相同的____数和不同的____数,这样的原子互称为____。