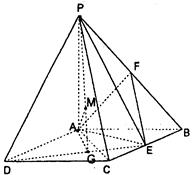
摘要:17. 如图.四棱锥中.平面.底面为矩形...为的中点. (Ⅰ)求证:, (Ⅱ)求三棱锥的体积, (Ⅲ)边上是否存在一点.使得平面.若存在.求出的长,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_540209[举报]
(本小题满分14分)
 如图,四棱锥
如图,四棱锥![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,平面
的中点,平面![]() 与
与![]() 的交点为
的交点为![]()
(Ⅰ)求![]() 的长度;
的长度;
(Ⅱ)求截面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(Ⅲ)求四棱锥![]() 的体积.
的体积.
(本小题满分14分)
如图, 在四棱锥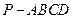 中,顶点
中,顶点 在底面
在底面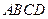 上的射影恰好落在
上的射影恰好落在 的中点
的中点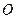 上,又∠
上,又∠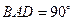 ,
,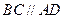 ,且
,且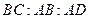
=1:2:2.
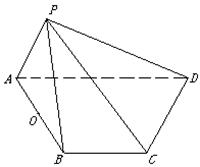
(1) 求证: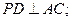
(2) 若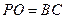 , 求直线
, 求直线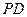 与
与 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面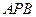 与平面
与平面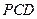 所成的角为
所成的角为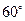 , 求
, 求 的值
的值
如图, 在四棱锥
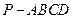 中,顶点
中,顶点 在底面
在底面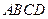 上的射影恰好落在
上的射影恰好落在 的中点
的中点 上,又∠
上,又∠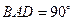 ,
,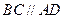 ,且
,且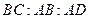
=1:2:2.

(1) 求证:
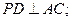
(2) 若
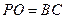 , 求直线
, 求直线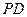 与
与 所成的角的余弦值;
所成的角的余弦值;(3) 若平面
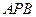 与平面
与平面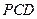 所成的角为
所成的角为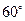 , 求
, 求 的值
的值(本小题满分14分)
如图:四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
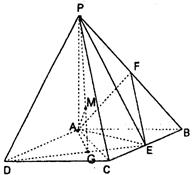
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在BC边的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,PA与平面PDE所成角的大小为45°
查看习题详情和答案>>
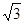 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.