摘要：解析:(Ⅰ)设椭圆长半轴长及半焦距分别为.由已知得 . 所以椭圆的标准方程为 (Ⅱ)设.其中.由已知及点在椭圆上可得 . 整理得.其中. (i)时.化简得 所以点的轨迹方程为.轨迹是两条平行于轴的线段. (ii)时.方程变形为.其中 当时.点的轨迹为中心在原点.实轴在轴上的双曲线满足的部分. 当时.点的轨迹为中心在原点.长轴在轴上的椭圆满足的部分, 当时.点的轨迹为中心在原点.长轴在轴上的椭圆,
网址：http://m.1010jiajiao.com/timu3_id_535390[举报]
已知椭圆的中心在原点，焦点在y轴上，焦距为4，离心率为
．
（Ⅰ）求椭圆的方程；
（Ⅱ）设椭圆在y轴的正半轴上的焦点为M，又点A和B在椭圆上，且M分有向线段
所成的比为2，求线段AB所在直线的方程．
查看习题详情和答案>>
| 2 |
| 3 |
（Ⅰ）求椭圆的方程；
（Ⅱ）设椭圆在y轴的正半轴上的焦点为M，又点A和B在椭圆上，且M分有向线段
. |
| AB |
已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为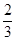
．
（1）求椭圆方程；
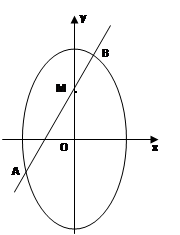
（2）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段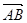
所成的比为2，求线段AB所在直线的方程．
（本题满分为12分）
已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为
．
（I）求椭圆方程；
（II）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段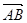
所成的比为2，求线段AB所在直线的方程．
．
所成的比为2，求线段AB所在直线的方程．
．
所成的比为2，求线段AB所在直线的方程．