题目内容
(本小题满分12分)
已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.
(I)求椭圆方程;
(II)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
(I)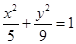 (II)
(II)
解析试题分析:(I)由题意知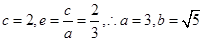 .
.
所以,所求椭圆方程为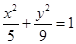 .
.
(2)设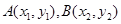 ,
,
由题意可知直线AB的斜率存在,设过A,B的直线方程为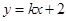 ,
,
则由  得
得 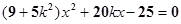 ,
,
故 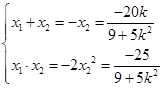 ,
,
由M分有向线段 所成的比为2,得
所成的比为2,得 ,
,
消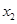 得
得 
解得 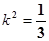 ,
,
所以, .
.
考点:本小题主要考查圆锥曲线的性质及应用.
点评:解决圆锥曲线问题,免不了要联立直线与圆锥曲线方程,这样运算量会比较大,要仔细运算,考查学生的运算求解能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 为抛物线
为抛物线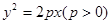 的焦点,点
的焦点,点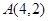 为抛物线内一定点,点
为抛物线内一定点,点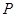 为抛物线上一动点,
为抛物线上一动点,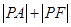 最小值为8.
最小值为8.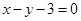 与抛物线交于
与抛物线交于 、
、 两点,求
两点,求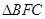 的面积.
的面积.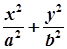 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
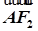 =2
=2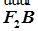 ,
,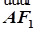 ·
·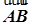 =
=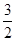 ,求椭圆的方程.
,求椭圆的方程.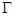 的方程为
的方程为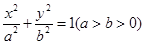 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点 的坐标;
的坐标; 交椭圆
交椭圆 、
、 两点,交直线
两点,交直线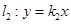 于点
于点 .若
.若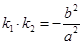 ,证明:
,证明: 的中点;
的中点;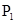 、
、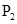 满足
满足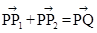 ,写出求作点
,写出求作点 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F (1,0),离心率为
(1,0),离心率为 ,P为左顶点。
,P为左顶点。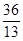 ,求直线AB的方程。
,求直线AB的方程。 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为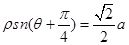 ,曲线
,曲线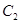 的参数方程为
的参数方程为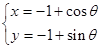 ,(
,(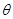 为参数,
为参数,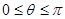 )。
)。 的取值范围。
的取值范围。 为抛物线
为抛物线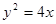 的焦点,
的焦点, 为抛物线上任意一点,已
为抛物线上任意一点,已 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于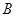 点,试判断过
点,试判断过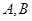 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。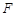 为抛物线
为抛物线 :
: 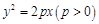 的焦点,
的焦点, 为抛物线
为抛物线 .
.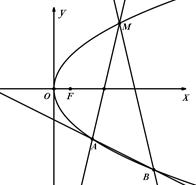
 的坐标;
的坐标;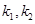 的两直线
的两直线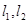 ,
, 与抛物线
与抛物线 ,
, 与抛物线
与抛物线 ,记直线
,记直线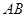 的斜率为
的斜率为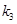 .
. ,试求
,试求 为定值.
为定值.