摘要:40.(命题人:如东丰利中学宋浩.审题人:如东丰利中学袁峰) 下面的一组图形为某一四棱锥S-ABCD的侧面与底面. (1)请画出四棱锥S-ABCD的示意图.是否存在一条侧棱SA垂直于底面ABCD?如果存在.请给出证明, (2)若SA⊥面ABCD.点E为AB的中点.点G为SC的中点.求证EG∥面SAD. 的条件下.求证:平面SEC⊥平面SCD, [解析](1)存在一条侧棱垂直于底面 证明:∵SA⊥AB.SA⊥AD.AB∩AD=A. ∴SA⊥面ABCD. (2)取SD的中点F.连接GF.AF.则GF∥EA. 又∵GF=CD=AB=AE.∴四边形ABCD为平行四边形. ∴AF∥EG. 又∵EG面SAD.AF面SAD. ∴EG ∥面SAD. (3)∵△SAD为等腰三角形.F为SD的中点.∴AF⊥SD. ∵SA⊥面ABCD.∴SA⊥CD. 又∵AD⊥CD.∴CD⊥面SAD. ∵AF面SAD.∴CD⊥AF.∴AF⊥面SCD. 由(2)知.AF∥EG.所以EG⊥面SAD. 又∵EG面SEC.∴面SEC⊥面SCD.
网址:http://m.1010jiajiao.com/timu3_id_533662[举报]
下面的一组图形为某一四棱锥S-ABCD的侧面与底面.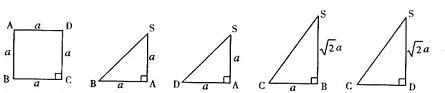
(I)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说理理由;
(II)若E为AB中点,求证:平面SEC⊥平面SCD. 查看习题详情和答案>>

(I)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说理理由;
(II)若E为AB中点,求证:平面SEC⊥平面SCD. 查看习题详情和答案>>
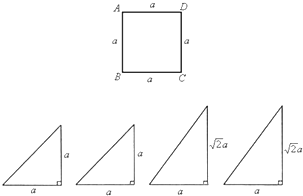 (2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.
(2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.(Ⅰ)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱SA垂直于底面ABCD?如果存在,请给出证明;
(Ⅱ)若E为AB中点,求证:平面SEC⊥平面SCD;
(Ⅲ)求二面角B-SC-D的大小.
下面的一组图形为某一四棱锥S-ABCD的侧面与底面.
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA⊥面ABCD,求证:平面SAC⊥平面SBD,并求点A到平面SBD的距离. 查看习题详情和答案>>

(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA⊥面ABCD,求证:平面SAC⊥平面SBD,并求点A到平面SBD的距离. 查看习题详情和答案>>


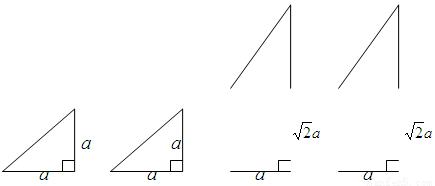
 面ABCD,E为AB中点,求证:面
面ABCD,E为AB中点,求证:面 面
面