题目内容
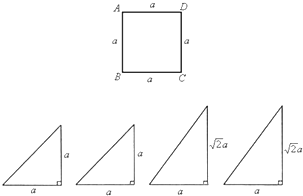 (2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.
(2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.(Ⅰ)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱SA垂直于底面ABCD?如果存在,请给出证明;
(Ⅱ)若E为AB中点,求证:平面SEC⊥平面SCD;
(Ⅲ)求二面角B-SC-D的大小.
分析:(I)根据已知中的侧面形状,易判断出SA⊥AB,SA⊥AD,进而根据线面垂直的判定定理,可得SA⊥面ABCD
(II)取SD中点F,SC的中点G,连结AF、FG、EG,先证出AF⊥面SCD,及四边形AEGF为平行四边形,进而得到EG⊥面SCD,最后由面面垂直的判定定理得到平面SEC⊥平面SCD
(III)过D作DH⊥SC于H,连结HB、BD,可得∴∠BHD为二面角B-SC-D的平面角,解Rt△SDC和△BHD可得答案.
(II)取SD中点F,SC的中点G,连结AF、FG、EG,先证出AF⊥面SCD,及四边形AEGF为平行四边形,进而得到EG⊥面SCD,最后由面面垂直的判定定理得到平面SEC⊥平面SCD
(III)过D作DH⊥SC于H,连结HB、BD,可得∴∠BHD为二面角B-SC-D的平面角,解Rt△SDC和△BHD可得答案.
解答:解:(I)存在一条侧棱SA⊥面ABCD,如图所示.
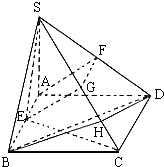
∵在△SAB中,SA⊥AB,
在△SAD中,SA⊥AD
又∵AB∩AD=A,AB,AD?面ABCD
∴SA⊥面ABCD…(4分)
(II)取SD中点F,SC的中点G,连结AF、FG、EG
∵SA⊥面ABCD,∴SA⊥CD
又∵CD⊥AD且SA∩AD=A
∴CD⊥面SAD
∴CD⊥AF
∵Rt△SAD中,SA=AD,
∴AF⊥SD
又∵CD∩SD=D,
∴AF⊥面SCD
∵FG∥CD,FG=
CD,AE∥CD,AE=
CD,
∴FG∥AE,FG=AE
∴四边形AEGF为平行四边形
∴EG∥AF
∴EG⊥面SCD
又∵EG?面SEC,
∴平面SEC⊥平面SCD…(9分)
(III)过D作DH⊥SC于H,连结HB、BD
∵△SBH≌△SDH
∴∠BHS=∠DHS=90°
∴BH⊥SC
∴∠BHD为二面角B-SC-D的平面角
Rt△SDC中,DH=
=
=
a
△BHD中,cos∠BHD=
=
=-
∴∠BHD=120°
∴二面角B-SC-D的大小为120°…(14分)

∵在△SAB中,SA⊥AB,
在△SAD中,SA⊥AD
又∵AB∩AD=A,AB,AD?面ABCD
∴SA⊥面ABCD…(4分)
(II)取SD中点F,SC的中点G,连结AF、FG、EG
∵SA⊥面ABCD,∴SA⊥CD
又∵CD⊥AD且SA∩AD=A
∴CD⊥面SAD
∴CD⊥AF
∵Rt△SAD中,SA=AD,
∴AF⊥SD
又∵CD∩SD=D,
∴AF⊥面SCD
∵FG∥CD,FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴FG∥AE,FG=AE
∴四边形AEGF为平行四边形
∴EG∥AF
∴EG⊥面SCD
又∵EG?面SEC,
∴平面SEC⊥平面SCD…(9分)
(III)过D作DH⊥SC于H,连结HB、BD
∵△SBH≌△SDH
∴∠BHS=∠DHS=90°
∴BH⊥SC
∴∠BHD为二面角B-SC-D的平面角
Rt△SDC中,DH=
| SD?DC |
| SC |
| ||
|
| ||
| 3 |
△BHD中,cos∠BHD=
| BH2+DH2-BD2 |
| 2?BH?DH |
(
| ||||||||||
2•
|
| 1 |
| 2 |
∴∠BHD=120°
∴二面角B-SC-D的大小为120°…(14分)
点评:本题考查的知识点是二面角的平面角及求法,平面与平面垂直的判定,解答(I)(II)的关键是熟练掌握空间线线垂直,线面垂直及面面垂直之间的相互转化,解答(III)的关键是确定二面角的平面角.

练习册系列答案
相关题目