题目内容
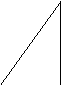
16、下面的一组图形为某一四棱锥S-ABCD的侧面与底面.

(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA⊥面ABCD,E为AB中点,求证面SEC⊥面SCD.

(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA⊥面ABCD,E为AB中点,求证面SEC⊥面SCD.
分析:(1)由 SA⊥AB,SA⊥AD 可得,存在一条侧棱SA垂直于底面.
(2)分别取SC、SD的中点G、F,可证AF∥EG.证明CD⊥AF,AF⊥SD,从而证明 AF⊥面SCD,故EG⊥面SCD,从而证得面SEC⊥面SCD.
(2)分别取SC、SD的中点G、F,可证AF∥EG.证明CD⊥AF,AF⊥SD,从而证明 AF⊥面SCD,故EG⊥面SCD,从而证得面SEC⊥面SCD.
解答: 解:(1)存在一条侧棱垂直于底面.
解:(1)存在一条侧棱垂直于底面.
证明:∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD.
(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG.
而由SA⊥面ABCD得 SA⊥CD,
又AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD.
 解:(1)存在一条侧棱垂直于底面.
解:(1)存在一条侧棱垂直于底面.证明:∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD.
(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG.
而由SA⊥面ABCD得 SA⊥CD,
又AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD.
点评:本题考查证明线面垂直、面面垂直的方法,体现了数形结合的数学思想,证明AF⊥面SCD是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
 | |||||
 |  | ||||
![]()
![]()
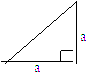 | 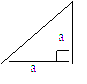 | ||||||
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA![]() 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)求点D到面SEC的距离。
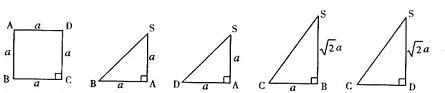
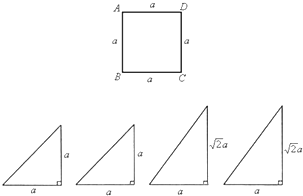 (2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.
(2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.