摘要:18. (命题人:启东中学李俊.审题人:启东中学曹瑞彬.原创) 设顶点为的抛物线交轴正半轴于.两点.交轴正半轴于 点.圆(圆心为)过..三点.恰好与轴相切. 求证:. 解:设..三点的坐标为...圆的圆心坐标为. 由韦达定理.知. 原点到圆D的切线为.所以 .即. 故. 点坐标为 . 由(1).. 设交轴于.要证与圆相切.即证 . 如果.那么与相似.. 所以只需证 .而 .. 所以 等价于 .即只需要证. 由..所以与圆相切.
网址:http://m.1010jiajiao.com/timu3_id_533640[举报]
(本题满分8分)
如图,抛物线![]() 的顶点在原点,对称轴是
的顶点在原点,对称轴是![]() 轴,并经过点
轴,并经过点![]() .
.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(II)设过点![]() 的直线交
的直线交![]() 轴于
轴于![]() 点,交抛物线
点,交抛物线![]() 于
于![]() 点,
点,![]()
 ①当
①当![]() 时,求
时,求![]() 的面积;
的面积;
②当![]() 时,求点
时,求点![]() 横坐标的取值范围.
横坐标的取值范围.
![]()
设斜率为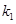 的直线
的直线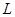 交椭圆
交椭圆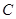 :
: 于
于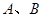 两点,点
两点,点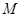 为弦
为弦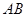 的中点,直线
的中点,直线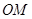 的斜率为
的斜率为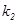 (其中
(其中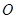 为坐标原点,假设
为坐标原点,假设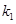 、
、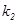 都存在).
都存在).
(1)求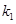 ×
×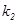 的值.
的值.
(2)把上述椭圆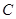 一般化为
一般化为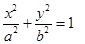 (
(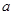 >
>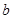 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想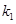 与
与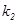 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线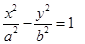 (
(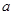 >0,
>0,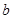 >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.
查看习题详情和答案>>
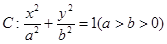 的左右焦点分别是
的左右焦点分别是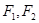 ,离心率
,离心率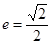 ,
,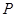 为椭圆上任一点,且
为椭圆上任一点,且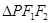 的最大面积为
的最大面积为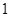 .
. 的方程;
的方程; 的直线
的直线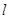 交椭圆
交椭圆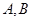 两点,且以
两点,且以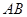 为直径的圆恒过原点
为直径的圆恒过原点 ,若实数
,若实数 满足条件
满足条件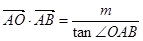 ,求
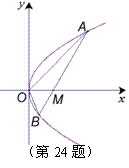
,求 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,