题目内容
设斜率为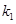 的直线
的直线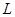 交椭圆
交椭圆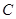 :
: 于
于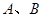 两点,点
两点,点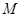 为弦
为弦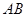 的中点,直线
的中点,直线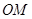 的斜率为
的斜率为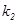 (其中
(其中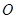 为坐标原点,假设
为坐标原点,假设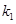 、
、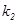 都存在).
都存在).
(1)求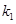 ×
×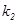 的值.
的值.
(2)把上述椭圆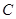 一般化为
一般化为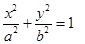 (
(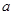 >
>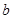 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想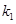 与
与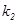 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线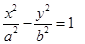 (
(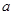 >0,
>0,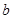 >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.
【答案】
(1)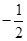
(2)略
【解析】解(一):(1)设直线方程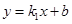 ,代入椭圆方程并整理得:
,代入椭圆方程并整理得:
 ,
,
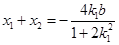 ,又中点M在直线上,所以
,又中点M在直线上,所以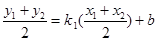 ,从而可得弦中点M的坐标为
,从而可得弦中点M的坐标为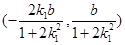 ,
,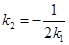 ,所以
,所以
解(二)设点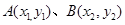 ,中点
,中点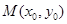 则
则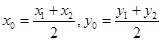

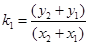
又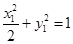 与
与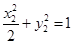 作差得
作差得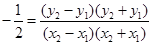 所以
所以
(2)对于椭圆,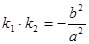
已知斜率为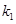 的直线
的直线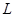 交双曲线
交双曲线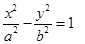 (
(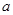 >0,
>0,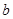 >0)于
>0)于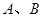 两点,点
两点,点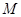 为弦
为弦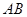 的中点,直线
的中点,直线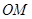 的斜率为
的斜率为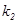 (其中
(其中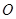 为坐标原点,假设
为坐标原点,假设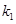 、
、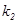 都存在).
都存在).
则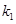 ×
×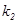 的值为
的值为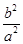 .
. 
(解一)、设直线方程为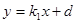 ,代入
,代入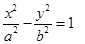 (
(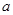 >0,
>0,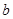 >0)方程并整理得:
>0)方程并整理得:
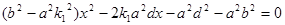 ,
,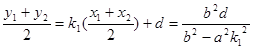 ,
,
所以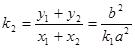 ,即
,即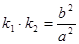
(解二)设点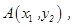
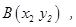 中点
中点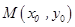
则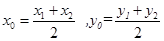
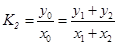
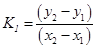
又因为点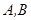 在双曲线上,则
在双曲线上,则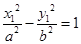 与
与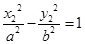 作差得
作差得
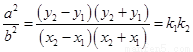 即
即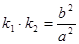

练习册系列答案
相关题目
 是椭圆
是椭圆 上一点,且点
上一点,且点 到椭圆的两个焦点距离之和为
到椭圆的两个焦点距离之和为 ;
;
 为椭圆的左顶点,直线
为椭圆的左顶点,直线 交
交 轴于点
轴于点 ,过
,过 的直线
的直线 交椭圆于
交椭圆于 两点,若
两点,若 ,求实数
,求实数 的直线
的直线 与椭圆
与椭圆 交于不同的两点,且这两个交点在
交于不同的两点,且这两个交点在 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为
轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为 B、
B、 C、
C、
 :
: 的左焦点
的左焦点 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于线段
相切于线段 .
. 及椭圆
及椭圆 :
: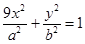 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 两点,设线段
两点,设线段 的中点为
的中点为 ,连结
,连结 ,试问当
,试问当 的直线交椭圆
的直线交椭圆 :
: 于
于 、
、 两点,其中
两点,其中 轴的垂线,垂足为
轴的垂线,垂足为 ,连结
,连结 并延长交椭圆
并延长交椭圆 ,求证:
,求证:
 是椭圆
是椭圆 的左焦点,
的左焦点,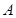 是椭圆短轴上的一个顶点,椭圆的离心率为
是椭圆短轴上的一个顶点,椭圆的离心率为 ,点
,点 在
在 轴上,
轴上, ,
,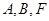 三点确定的圆
三点确定的圆 恰好与直线
恰好与直线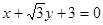 相切.
相切.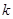
 的直线
的直线 交椭圆于
交椭圆于 两点,
两点, 为线段
为线段 的中点,设
的中点,设 为椭圆中心,射线
为椭圆中心,射线 交椭圆于点
交椭圆于点 ,若
,若 ,若存在求
,若存在求