摘要:22. 数列的通项是关于的不等式的解集中整数的个数. . (1)求数列的通项公式, (2) 若.求的和, (3) 求证:对且 恒有.
网址:http://m.1010jiajiao.com/timu3_id_533517[举报]
(本小题满分14分)
已知点集![]() ,其中
,其中![]() ,点列
,点列![]() (
(![]() )在L中,
)在L中,![]() 为L与y轴的交点,数列
为L与y轴的交点,数列![]() 是公差为1的等差数列.
是公差为1的等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() 令
令![]() ,试写出
,试写出![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)若![]() 给定奇数m(m为常数,
给定奇数m(m为常数,![]() ).是否存在
).是否存在![]() ,使得
,使得![]() ,若存在,求出k的值;若不存在,请说明理由.
,若存在,求出k的值;若不存在,请说明理由.
(本题满分14分)已知数列![]() 中,
中,![]() 且点
且点![]() 在直线
在直线![]() 上. (1)求数列
上. (1)求数列![]() 的通项公式; (2)若函数
的通项公式; (2)若函数![]() 求函数
求函数![]() 的最小值; (3)设
的最小值; (3)设![]() 表示数列
表示数列![]() 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于![]() 的整式
的整式![]() ,使得
,使得![]() 对于一切不小于2的自然数
对于一切不小于2的自然数![]() 恒成立? 若存在,写出
恒成立? 若存在,写出![]() 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本题满分14分)已知数列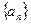 中,
中,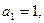 且点
且点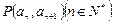 在直线
在直线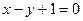 上.
上.
(1)求数列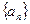 的通项公式;
的通项公式;
(2)若函数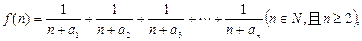 求函数
求函数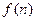 的最小值;
的最小值;
(3)设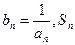 表示数列
表示数列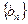 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于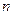 的整式
的整式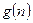 ,使得
,使得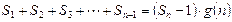 对于一切不小于2的自然数
对于一切不小于2的自然数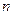 恒成立? 若存在,写出
恒成立? 若存在,写出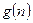 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
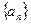 中,
中,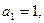 且点
且点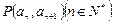 在直线
在直线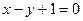 上.
上.(1)求数列
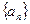 的通项公式;
的通项公式;(2)若函数
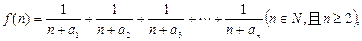 求函数
求函数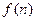 的最小值;
的最小值;(3)设
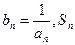 表示数列
表示数列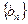 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于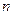 的整式
的整式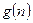 ,使得
,使得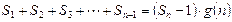 对于一切不小于2的自然数
对于一切不小于2的自然数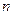 恒成立? 若存在,写出
恒成立? 若存在,写出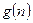 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.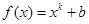 (常数
(常数 )的图像过点
)的图像过点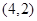 、
、 两点.
两点. 的解析式;
的解析式; 的图像与函数
的图像与函数 对称,若不等式
对称,若不等式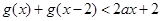 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是函数
是函数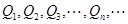 是
是 正半轴上的点列,
正半轴上的点列, 为坐标原点,
为坐标原点,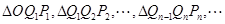 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是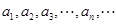 ,探求数列
,探求数列 的通项公式,并说明理由.
的通项公式,并说明理由.