网址:http://m.1010jiajiao.com/timu3_id_532689[举报]
由已知得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
答案:C.
【命题立意】:本题考查归纳推理以及函数的周期性和对数的运算.
查看习题详情和答案>>解:由cx2-bx+a>0且x≠0,所以
| (c×2-bx+a) |
| x2 |
| 1 |
| x |
| b |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
参考上述解法,解决如下问题:已知关于x的不等式
| b |
| (x+a) |
| (x+c) |
| (x+d) |
| bx |
| (ax-1) |
| (cx-1) |
| (dx-1) |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
设函数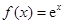 ,其中
,其中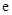 为自然对数的底数.
为自然对数的底数.
(1)求函数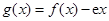 的单调区间;
的单调区间;
(2)记曲线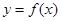 在点
在点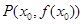 (其中
(其中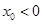 )处的切线为
)处的切线为 ,
, 与
与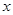 轴、
轴、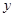 轴所围成的三角形面积为
轴所围成的三角形面积为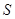 ,求
,求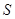 的最大值.
的最大值.
【解析】第一问利用由已知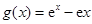 ,所以
,所以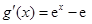 ,
,
由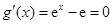 ,得
,得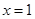 ,
所以,在区间
,
所以,在区间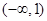 上,
上,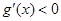 ,函数
,函数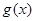 在区间
在区间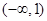 上单调递减;
在区间
上单调递减;
在区间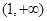 上,
上, ,函数
,函数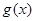 在区间
在区间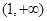 上单调递增;
上单调递增;
第二问中,因为 ,所以曲线
,所以曲线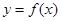 在点
在点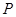 处切线为
处切线为 :
: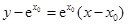 .
.
切线 与
与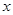 轴的交点为
轴的交点为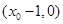 ,与
,与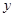 轴的交点为
轴的交点为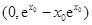 ,
,
因为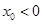 ,所以
,所以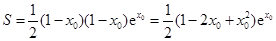 ,
,
 , 在区间
, 在区间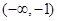 上,函数
上,函数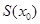 单调递增,在区间
单调递增,在区间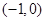 上,函数
上,函数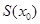 单调递减.所以,当
单调递减.所以,当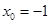 时,
时,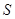 有最大值,此时
有最大值,此时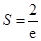 ,
,
解:(Ⅰ)由已知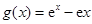 ,所以
,所以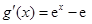 ,
由
,
由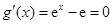 ,得
,得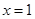 , 所以,在区间
, 所以,在区间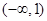 上,
上,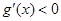 ,函数
,函数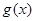 在区间
在区间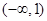 上单调递减;
上单调递减;
在区间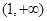 上,
上, ,函数
,函数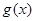 在区间
在区间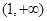 上单调递增;
上单调递增;
即函数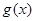 的单调递减区间为
的单调递减区间为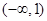 ,单调递增区间为
,单调递增区间为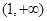 .
.
(Ⅱ)因为 ,所以曲线
,所以曲线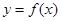 在点
在点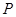 处切线为
处切线为 :
: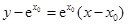 .
.
切线 与
与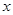 轴的交点为
轴的交点为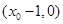 ,与
,与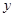 轴的交点为
轴的交点为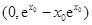 ,
,
因为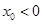 ,所以
,所以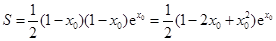 ,
,
 , 在区间
, 在区间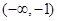 上,函数
上,函数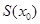 单调递增,在区间
单调递增,在区间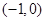 上,函数
上,函数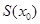 单调递减.所以,当
单调递减.所以,当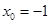 时,
时,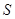 有最大值,此时
有最大值,此时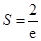 ,
,
所以,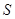 的最大值为
的最大值为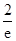
查看习题详情和答案>>
 ,
, ,
, 为常数,离心率为
为常数,离心率为 的双曲线
的双曲线 :
: 上的动点
上的动点 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为 ,抛物线
,抛物线 :
:
 的焦点与双曲线
的焦点与双曲线 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线 :
: (
( 为负常数)上任意一点
为负常数)上任意一点 向抛物线
向抛物线 引两条切线,切点分别为
引两条切线,切点分别为 、
、 ,坐标原点
,坐标原点 恒在以
恒在以 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
第二问中, 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得:
借助于根与系数的关系得到即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即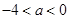
解:(Ⅰ)由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
(Ⅱ)设 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得: ,
,
即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即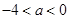
查看习题详情和答案>>
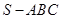 中,平面
中,平面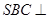 平面
平面 ,
,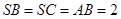 ,
,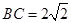 ,
,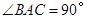 ,
,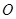 为
为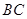 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.
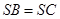 ,
,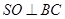
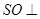 平面
平面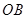 、
、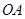 、
、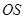 为
为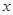 ,
,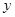 ,
,
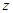 轴建立直角坐标系得
轴建立直角坐标系得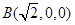 ,
,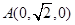 ,
,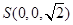 ,
,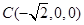 ,
,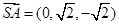 ,
,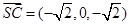 ,
, 而
而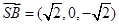 ,故点B到平面
,故点B到平面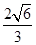
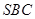 的法向量
的法向量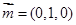 ,平面
,平面