摘要:2.已知圆:. (1)直线过点.且与圆交于.两点.若.求直线的方程, (2)过圆上一动点作平行于轴的直线.设与轴的交点为.若向量.求动点的轨迹方程.并说明此轨迹是什么曲线. 解(Ⅰ)①当直线垂直于轴时.则此时直线方程为.与圆的两个交点坐标为和 其距离为.满足题意 ②若直线不垂直于轴.设其方程为.即 设圆心到此直线的距离为.则.得∴..故所求直线方程为 综上所述.所求直线为或 (Ⅱ)设点的坐标为.点坐标为则点坐标是 ∵.∴ 即. 又∵.∴由已知.直线m //ox轴.所以. ∴点的轨迹方程是. 轨迹是焦点坐标为.长轴为8的椭圆.并去掉两点.
网址:http://m.1010jiajiao.com/timu3_id_531937[举报]
 :
: .
. 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若 ,求直线
,求直线 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 轴的交点为
轴的交点为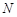 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.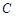 :
: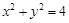 .
. 过点
过点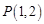 ,且与圆
,且与圆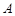 、
、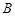 两点,若
两点,若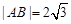 ,求直线
,求直线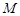 作平行于
作平行于 轴的直线
轴的直线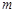 ,设
,设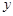 轴的交点为
轴的交点为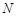 ,若向量
,若向量 ,求动点
,求动点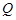 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.