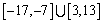题目内容
已知圆![]() :
:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(1)直线方程为![]()
(2)∴![]() 点的轨迹方程是
点的轨迹方程是![]() ,轨迹是焦点坐标为
,轨迹是焦点坐标为![]() ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉![]() 两点。
两点。
解析:
(Ⅰ)①当直线![]() 垂直于
垂直于![]() 轴时,则此时直线方程为
轴时,则此时直线方程为![]() ,
,
![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,其距离为
,其距离为![]() ,满足题意……… 2分
,满足题意……… 2分
②若直线![]() 不垂直于
不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,
,
即![]() …………………………………………………… 3分
…………………………………………………… 3分
设圆心到此直线的距离为![]() ,则
,则![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
故所求直线方程为![]() ……………………………………5分
……………………………………5分
综上所述,所求直线为![]() 或
或![]() …………………… 6分
…………………… 6分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标是
点坐标是![]() …… 7分
…… 7分
∵![]() ,∴
,∴![]() 即
即![]() ,
,![]()
![]() …………9分
…………9分
又∵![]() ,∴
,∴![]() …………………………… 10分
…………………………… 10分
由已知,直线m ∥ox轴,所以,![]() ,…………………………… 11分
,…………………………… 11分
∴![]() 点的轨迹方程是
点的轨迹方程是![]() ,…………………… 12分
,…………………… 12分
轨迹是焦点坐标为![]() ,长轴为8的椭圆,
,长轴为8的椭圆,
并去掉![]() 两点。
两点。

练习册系列答案
相关题目

 及直
及直
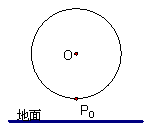 (8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
(8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为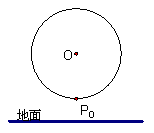 (8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
(8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为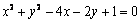 ,直线
,直线 ,圆上只有两个点到直
,圆上只有两个点到直 的距离为1,则k的取值范围( )
的距离为1,则k的取值范围( ) B.
B. C.
C. D.
D.