题目内容
已知圆 :
: .
.
⑴直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
⑵过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为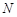 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
【答案】
(1)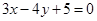 或
或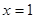 .
.
(2)轨迹是焦点坐标为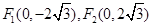 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉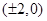 两点.
两点.
【解析】⑴①当直线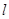 垂直于
垂直于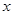 轴时,则此时直线方程为
轴时,则此时直线方程为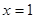 ,
,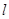 与圆的两个交点坐标为
与圆的两个交点坐标为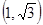 和
和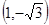 ,其距离为
,其距离为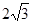 ,满足题意.
,满足题意.
②若直线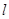 不垂直于
不垂直于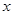 轴,设其方程为
轴,设其方程为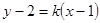 ,即
,即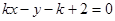
设圆心到此直线的距离为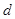 ,则
,则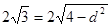 ,得
,得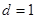 ∴
∴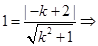
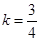 ,
,
故所求直线方程为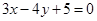 综上所述,所求直线为
综上所述,所求直线为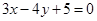 或
或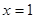 .
.
⑵设点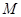 的坐标为
的坐标为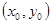 ,
, 点坐标为
点坐标为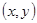 , 则
, 则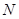 点坐标是
点坐标是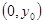 .
.
∵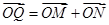 ,∴
,∴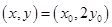 即
即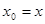 ,
,
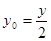
又∵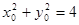 ,∴
,∴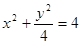 由已知,直线m //ox轴,所以,
由已知,直线m //ox轴,所以,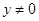 ,
,
∴ 点的轨迹方程是
点的轨迹方程是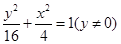 ,
,
轨迹是焦点坐标为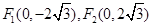 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉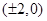 两点.
两点.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
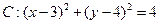 ,直线
,直线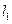 过定点A(1,0),若
过定点A(1,0),若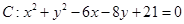 ,直线
,直线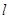 过定点
过定点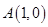 .
.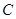 的坐标和圆的半径
的坐标和圆的半径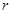 ;
;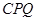 面积的最大值,并求此时
面积的最大值,并求此时 ,直线
,直线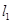 过定点A(1,0).
过定点A(1,0).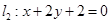 的交点为N,求证:
的交点为N,求证: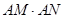 为定值.
为定值.