摘要： 2．, 3. 4 4． a≥-8,5. 6.解析:易知.且当x∈时.为增函数．又由.得.故 |.于是．选B．
网址：http://m.1010jiajiao.com/timu3_id_531304[举报]
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
附：
,其中n＝a＋b＋c＋d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.
附：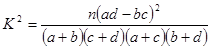
,其中n＝a＋b＋c＋d.)
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
附：
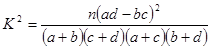,其中n＝a＋b＋c＋d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
现代社会对破译密码的要求越来越高，有一种密码把英文的明文（真实文）按字母分解，其中英文的a、b、c、…、z的26个字母（不论大小写）依次对应1、2、3、…、26这26个自然数，见表格：
给出如下一个变换公式：x′=
将明文转换成密文，如6→
+13=16即f变为p；9→
=5即i变为e．
按上述规定，明文good的密文是
查看习题详情和答案>>
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
将明文转换成密文，如6→
| 6 |
| 2 |
| 9+1 |
| 2 |
按上述规定，明文good的密文是
dhho
dhho
，密文gawqj的明文是maths
maths
．
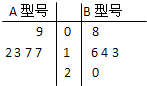某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：（1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率PA、PB；
（2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
表一
| 等级 利润 产品 |
一等品 | 二等品 |
| A型 | 4（万元） | 3（万元） |
| B型 | 3（万元） | 2（万元） |
| 项目 用量 产品 |
配件（件） | 资金（万元） |
| A型 | 6 | 4 |
| B型 | 2 | 8 |