摘要: 如图.椭圆:....为椭圆的顶点. (Ⅰ)若椭圆上的点到焦点距离的最大值为.最小值为. 求椭圆方程 (Ⅱ)已知:直线相交于.两点(不是椭圆的左右顶点).并满足.试研究:直线是否过定点? 若过定点.请求出定点坐标.若不过定点.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_529930[举报]
(本小题满分12分)
如图,设抛物线C1:![]() 的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率
的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率![]() 的椭圆C2与抛物线C1在x轴上方的交点为P。
的椭圆C2与抛物线C1在x轴上方的交点为P。
当m = 1时,求椭圆C2的方程;
 当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在
当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在![]() 上的一系列圆,它们的圆心纵坐标分别为a1,a2……an,已知a1 = 6,a1 > a2 >……> an > 0,又⊙Ck(k = 1,2,…,n)都与y轴相切,且顺次逐个相邻外切,求数列{an}的通项公式.
上的一系列圆,它们的圆心纵坐标分别为a1,a2……an,已知a1 = 6,a1 > a2 >……> an > 0,又⊙Ck(k = 1,2,…,n)都与y轴相切,且顺次逐个相邻外切,求数列{an}的通项公式.
|
 (本小题满分12分) 如图,已知椭圆
(本小题满分12分) 如图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]()
![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,
且![]() 求证:直线
求证:直线![]() 过定点,并求出该定点
过定点,并求出该定点![]() 的坐标.
的坐标.
(本小题满分12分)
如图,在直角坐标系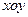 中,已知椭圆
中,已知椭圆 :
: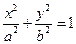
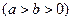 的离心率
的离心率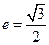 ,左、右两个焦点分别为
,左、右两个焦点分别为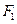 、
、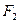 。过右焦点
。过右焦点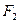 且与
且与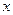 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交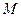 、
、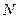 两点,且
两点,且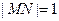 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左顶点为
的左顶点为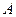 ,下顶点为
,下顶点为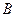 ,动点
,动点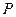 满足
满足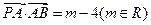 ,试求点
,试求点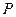 的轨迹方程,使点
的轨迹方程,使点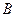 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
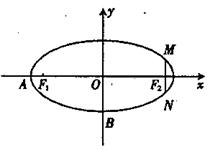
如图,在直角坐标系
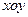 中,已知椭圆
中,已知椭圆 :
: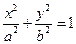
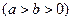 的离心率
的离心率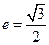 ,左、右两个焦点分别为
,左、右两个焦点分别为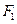 、
、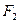 。过右焦点
。过右焦点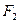 且与
且与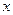 轴垂直的直线与椭圆
轴垂直的直线与椭圆 相交
相交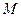 、
、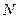 两点,且
两点,且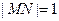 .
.(1)求椭圆
 的方程;
的方程;(2)设椭圆
 的左顶点为
的左顶点为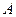 ,下顶点为
,下顶点为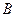 ,动点
,动点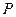 满足
满足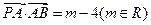 ,试求点
,试求点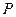 的轨迹方程,使点
的轨迹方程,使点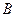 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.
 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补. 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.