题目内容
(本小题满分12分)
如图，设抛物线C1：
的准线与x轴交于F1，焦点为F2；以F1，F2为焦点，离心率
的椭圆C2与抛物线C1在x轴上方的交点为P。
当m = 1时，求椭圆C2的方程；
当△PF1F2的边长恰好是三个连续的自然数时，求抛物线方程；此时设⊙C1、⊙C2……⊙Cn是圆心在上的一系列圆，它们的圆心纵坐标分别为a1，a2……an，已知a1 = 6，a1 > a2 >……> an > 0，又⊙Ck（k = 1，2，…，n）都与y轴相切，且顺次逐个相邻外切，求数列{an}的通项公式．
|
解：(1) 当
时， 
，则
设椭圆方程为
，则
又
，所以
所以椭圆C2方程为
4分
(2) 因为
，，则
，
，设椭圆方程为
由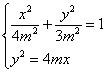
，得
即
，得
代入抛物线方程得
，
即
，
，
因为
的边长恰好是三个连续的自然数，所以
6分
此时抛物线方程为
， 7分
设
，则由题
∴ 
∴ 
∴ 
∴ 
∴ 
10分
即
是以
为公差，首项
的等差数列
∴ 
∴ 
12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
