题目内容
 如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,则异面直线BC与PA所成角的余弦值是( )
如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,则异面直线BC与PA所成角的余弦值是( )分析:以O为坐标原点,OA为x轴,OB为y轴,OP为z轴建立空间直角坐标系,根据几何图形的性质给出相关点的坐标,再求出向量
,
的坐标表示,利用向量坐标运算求异面直线所成角的余弦值.
| BC |
| PA |
解答: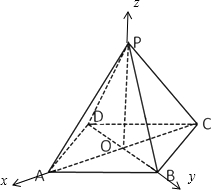 解:以O为坐标原点,OA为x轴,OB为y轴,OP为z轴建立空间直角坐标系,
解:以O为坐标原点,OA为x轴,OB为y轴,OP为z轴建立空间直角坐标系,
∵PO⊥平面ABCD,∴OB为PB在平面ABCD内的射影,∴∠PBO为PB与平面ABCD所成的角,即∠PBO=60°,
又底面是边长为2的菱形,∠DAB=60°,∴BD=2,OB=1,OP=
,OA=
,
∴B(0,1,0),C(-
,0,0),P(0,0,
),A(
,0,0),
∴
=(-
,-1,0),
=(
,0,-
),
∴cos<
,
>=
=
=-
.
∴异面直线BC与PA所成角的余弦值是
.
故选B.
 解:以O为坐标原点,OA为x轴,OB为y轴,OP为z轴建立空间直角坐标系,
解:以O为坐标原点,OA为x轴,OB为y轴,OP为z轴建立空间直角坐标系,∵PO⊥平面ABCD,∴OB为PB在平面ABCD内的射影,∴∠PBO为PB与平面ABCD所成的角,即∠PBO=60°,
又底面是边长为2的菱形,∠DAB=60°,∴BD=2,OB=1,OP=
| 3 |
| 3 |
∴B(0,1,0),C(-
| 3 |
| 3 |
| 3 |
∴
| BC |
| 3 |
| PA |
| 3 |
| 3 |
∴cos<
| BC |
| PA |
| ||||
|
|
| -3 | ||
2×
|
| ||
| 4 |
∴异面直线BC与PA所成角的余弦值是
| ||
| 4 |
故选B.
点评:本题考查了异面直线所成角的求法,本题采用了空间向量坐标运算求异面直线所成角的余弦值,另外本题也可通过作角、证角、求角解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
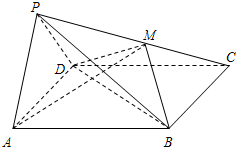 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.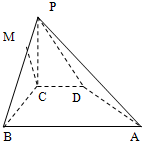 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB