题目内容
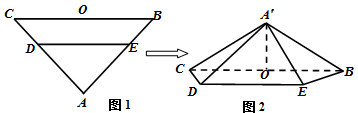
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱锥A′-BCDE.若A′O⊥平面BCDE,则A′D与平面A′BC所成角的正弦值等于( )
| 2 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:取DE中点H,则OH⊥OB.以O为坐标原点,OH、OB、OA'分别为x、y、z轴,建立空间直角坐标系,利用向量法能注出A′D与平面A′BC所成角的正弦值.
解答: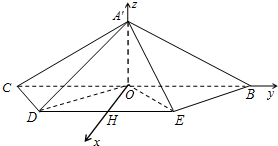 解:取DE中点H,则OH⊥OB.
解:取DE中点H,则OH⊥OB.
以O为坐标原点,OH、OB、OA′分别为x、y、z轴,建立空间直角坐标系,
∵等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=
,O为BC的中点,
∴A′′(0,0,
),D(1,-2,0),
∴
=(1,-2,-
),
∵平面A′BC的法向量
=(1,0,0),
设A′D与平面A′BC所成角为θ,
∴sinθ=|cos<
,
>|=|
|=
.
故选:D.
 解:取DE中点H,则OH⊥OB.
解:取DE中点H,则OH⊥OB.以O为坐标原点,OH、OB、OA′分别为x、y、z轴,建立空间直角坐标系,
∵等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=
| 2 |
∴A′′(0,0,
| 3 |
∴
| A′D |
| 3 |
∵平面A′BC的法向量
| n |
设A′D与平面A′BC所成角为θ,
∴sinθ=|cos<
| A′D |
| n |
| 1 | ||
|
| ||
| 4 |
故选:D.
点评:本题考查直线与平面所成角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
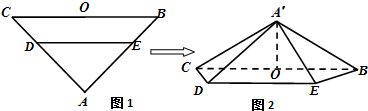 如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,

 ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′-BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′-BCDE,其中A′O= .
.