摘要：9． 如图所示.四棱锥P-ABCD的底面积ABCD是边长为1的菱形.∠BCD＝60°.E是CD的中点.PA⊥底面积ABCD.PA＝. (Ⅰ)证明:平面PBE⊥平面PAB, (Ⅱ)求二面角A-BE-P的大小. 解 解法一(Ⅰ)如图年示.连结BD.由ABCD是菱形且∠BCD＝60°知.ΔBCD是等边三角形.因为E是CD的中点.所以BE⊥CD.又AB∥CD.所以BE⊥AB.又因为PA⊥平面ABCD.BE平面ABCD.所以PA⊥BE.而PA∩AB＝A.因此BE⊥平面PAB. 又BE平面PBE.所以平面PBE⊥平面PAB. 知.BE⊥平面PAB.PB平面PAB.所以PB⊥BE. 又AB⊥BE.所以∠PBA是二面角A-BE-P的平面角. 在RtΔPAB中.tan∠PBA＝.∠PBA＝60°. 故二面角A-BE-P的大小是60°. 解法二 如图所示.以A为原点.建立空间直角坐标系.则相关各点的坐标分别是A.B.C().D().P().E(). (Ⅰ)因为.平面PAB的一个法向量是＝.所以和共线.从而BE⊥平面PAB.又因为BE平面BEF.所以平面PBE⊥平面PAB. (Ⅱ)易知=(1,0,-), =(0,,0), 设=(x1,y1,z1)是平面PBE的一个法向量.则有 所以y1=0,x1=z1.故可取=(,0,1). 而平面ABE的一个法向量是=. 于是.cos＜,＞＝. 故二面角A-BE-P的大小是
网址：http://m.1010jiajiao.com/timu3_id_527948[举报]
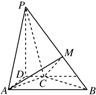如图所示，四棱锥P-ABCD中，PD⊥平面ABCD，PA与平面ABCD所成的角为60°，在四边形ABCD中，∠D=∠DAB=90°，AB=4，CD=1，AD=2．（1）建立适当的坐标系，并写出点B，P的坐标；
（2）求异面直线PA与BC所成角的余弦值． 查看习题详情和答案>>
（2013•怀化二模）如图所示，四棱锥P-ABCD，底面ABCD是边长为2的正方形，PA⊥面ABCD，PA=2，过点A作AE⊥PB，AF⊥PC，连接EF．（1）求证：PC⊥面AEF；
（2）若面AEF交侧棱PD于点G（图中未标出点G），求多面体P-AEFG的体积．
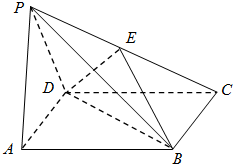如图所示，四棱锥P-ABCD中，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，∠BAD=60°，E为PC的中点，（1）求证：PA∥平面BDE；
（2）求证：PB⊥AD；
（3）（文科）求三棱锥C-PDB的体积．
（3）（理科） 求直线PC与平面ABCD所成角的正切值．
如图所示，四棱锥P-ABCD的底面ABCD为一直角梯形，其中AB⊥AD，CD⊥AD，CD=AD=PA=2AB，PA⊥底面ABCD，E是PC的中点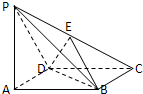
如图所示的四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，E为PC的中点，求证：