摘要：等边△ABC中,边长为2,则·的值为 ( ) A.4 B.-4 C.2 D.-2
网址：http://m.1010jiajiao.com/timu3_id_527754[举报]
下列正确命题的序号为
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
，则实数t的值为5
（3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
．
查看习题详情和答案>>
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
，则实数t的值为5 （3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
．
查看习题详情和答案>>
下列正确命题的序号为______
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
，则实数t的值为5
（3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
．
查看习题详情和答案>>
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
| 1 |
| 5 |
（3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
| 1 |
| 2 |
下列正确命题的序号为
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
，则实数t的值为5
（3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
．
查看习题详情和答案>>
（2）（4）
（2）（4）
（1）若直线l1⊥l2，则他们的斜率之积为-1
（2）已知等比数列{an}的前n项和Sn=t•5n-2-
| 1 |
| 5 |
（3）若直线x+ay-a=0与直线ax-（2a-3）y-1=0垂直，则a的值为2
（4）在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
| 1 |
| 2 |
（坐标系与参数方程选做题）在极坐标系中，定点A（2，π），动点B在直线ρsin(θ+
)=
上运动，则线段AB的最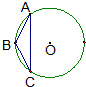
短长度为
（不等式选讲选做题）设函数f（x）=|x-1|+|x-2|，则f（x）的最小值为
（几何证明选讲选做题） 如图所示，等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，则三角形ABC的面积是 ．
查看习题详情和答案>>
| π |
| 4 |
| ||
| 2 |
短长度为（不等式选讲选做题）设函数f（x）=|x-1|+|x-2|，则f（x）的最小值为
（几何证明选讲选做题） 如图所示，等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，则三角形ABC的面积是
请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．（1）选修4-1：几何证明选讲
如图，在△ABC中，D是AC的中点，E是BD的中点，AE的延长线交BC于F．
（Ⅰ）求
| BF |
| FC |
（Ⅱ）若△BEF的面积为S1，四边形CDEF的面积为S2，求S1：S2的值．
（2）选修4-4：坐标系与参数方程
以直角坐标系的原点O为极点，a=
| π |
| 6 |
| π |
| 6 |
（ I）写出直线l的参数方程；
（ II）设l与圆ρ=2相交于两点A、B，求点P到A、B两点的距离之积．
（3）选修4-5：不等式选讲
已知函数f（x）=|2x+1|+|2x-3|．
（I）求不等式f（x）≤6的解集；
（II）若关于x的不等式f（x）＞a恒成立，求实数a的取值范围． 查看习题详情和答案>>