题目内容
(坐标系与参数方程选做题)在极坐标系中,定点A(2,π),动点B在直线ρsin(θ+| π |
| 4 |
| ||
| 2 |
 短长度为
短长度为(不等式选讲选做题)设函数f(x)=|x-1|+|x-2|,则f(x)的最小值为
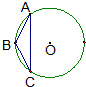
(几何证明选讲选做题) 如图所示,等腰三角形ABC的底边AC长为6,其外接圆的半径长为5,则三角形ABC的面积是
分析:(1)先利用三角函数的和角公式展开曲线C的极坐标方程的左式,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.将直线的极坐标方程化成直角坐标方程,再在直角坐标系中算出点到直线的距离,即线段AB的最短长度.
(2)先看1≤x≤2求得f(x)的值,再看x<1时,f(x)的解析式为直线方程,单调减,进而求得函数的值域;最后看x>2时,函数的解析式为直线方程,单调增,利用x的范围判断出函数的值域;最后综合求得答案.
(3)如图由等腰三角形的外心在三角形的底边的高上,根据勾股定理求出OD的长,进一步求出BD的长,根据三角形的面积公式即可求出答案.
(2)先看1≤x≤2求得f(x)的值,再看x<1时,f(x)的解析式为直线方程,单调减,进而求得函数的值域;最后看x>2时,函数的解析式为直线方程,单调增,利用x的范围判断出函数的值域;最后综合求得答案.
(3)如图由等腰三角形的外心在三角形的底边的高上,根据勾股定理求出OD的长,进一步求出BD的长,根据三角形的面积公式即可求出答案.
解答:解:(1)直线 ρsin(θ+
)=
的直角坐标方程为:
x+y-1=0,
定点A(2,π)的直角坐标(-2,0),
它到直线的距离:
d=
=
.
则线段AB的最短长度为
.
故答案为:
.
解:(2)当1≤x≤2时,f(x)=2-x+x-1=1
当x<1时,f(x)=1-x-x+2=-2x+1>1
当x>2时,f(x)=x-1+x-2=2x-3>1
∴函数f(x)的最小值为1
故答案为:1
解:(3)连接OB交AC于D,连接OC,
∵圆O是等腰三角形的外接圆,O是外心,
∴BD⊥AC,AD=DC=3,
如图,可求OD=4,
BD=5-4=1,
∴S△ABC=
AC•BD=
×6×1=3;
故答案为:3.
| π |
| 4 |
| ||
| 2 |
x+y-1=0,
定点A(2,π)的直角坐标(-2,0),
它到直线的距离:
d=
| |-2-1| | ||
|
3
| ||
| 2 |
则线段AB的最短长度为
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
解:(2)当1≤x≤2时,f(x)=2-x+x-1=1
当x<1时,f(x)=1-x-x+2=-2x+1>1
当x>2时,f(x)=x-1+x-2=2x-3>1
∴函数f(x)的最小值为1
故答案为:1
解:(3)连接OB交AC于D,连接OC,
∵圆O是等腰三角形的外接圆,O是外心,
∴BD⊥AC,AD=DC=3,
如图,可求OD=4,
BD=5-4=1,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:(1)本小题主要考查简单曲线的极坐标方程,属于基础题.能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
(2)本题主要考查了函数的值域问题.解题过程采用了分类讨论的思想,也可采用数形结合的方法,画出函数的图象,观察出函数的最小值.
(3)本题主要考查了三角形的外接圆和外心,等腰三角形的性质,勾股定理,三角形的面积等知识点,解此题的关键是求出高BD的长度.此题用的数学思想是分类讨论思想.题目较好.
(2)本题主要考查了函数的值域问题.解题过程采用了分类讨论的思想,也可采用数形结合的方法,画出函数的图象,观察出函数的最小值.
(3)本题主要考查了三角形的外接圆和外心,等腰三角形的性质,勾股定理,三角形的面积等知识点,解此题的关键是求出高BD的长度.此题用的数学思想是分类讨论思想.题目较好.

练习册系列答案
相关题目