摘要：重点:运用诱导公式.把求任意角的三角函数值问题转化为求0°-90°间角的三角函数值的问题.任意角的三角函数. 难点:对诱导公式中符号的确定 [典型例题] [例1] 设.求的值. 解: 方法一: ∵ ∴ 原式 方法二: 原式 [例2] 设求的值. 解: ∵ ∴ ∴ [例3] 已知.求的值. 解:∵ ∴ 又 ∴ 原式 [例4] 已知.为第三象限角.求的值. 解:又 ∵ 是第三象限角. ∴ ∴ ∵ ∴ 原式 [例5] 已知.是关于x的方程的两实根.且.求的值. 解:∵ .是方程的两实根 ∴ ∴ ∵ ∴ ... ∴ ∴ ∴ 方程化为 ∴ 即 ∴ ∴ . ∴ [例6] 已知.求的值. 解:由已知等式变形可得 即 ∴ ∴ ∴ [例7] 已知:.求和的值. 解:由平方.可得 ∴ [例8] 已知.求证: 证:由已知 ∴ [模拟试题]
网址：http://m.1010jiajiao.com/timu3_id_526848[举报]
要得到函数y=2cos(2x+
)的图象．可以由诱导公式先把它变成y=2sin（
）然后由y=sinx的图象先向
平移
个单位，再把各点的纵坐标不变，横坐标变为原来的
倍，最后把各点的横坐标不变，纵坐标变为原来的
倍，就可以得到y=2cos(2x+
)的图象．
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
要得到函数y=2cos(2x+
)的图象．可以由诱导公式先把它变成y=2sin（
______）然后由y=sinx的图象先向
______平移
______个单位，再把各点的纵坐标不变，横坐标变为原来的
______倍，最后把各点的横坐标不变，纵坐标变为原来的
______倍，就可以得到y=2cos(2x+
)的图象．
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
要得到函数y=2cos(2x+
)的图象．可以由诱导公式先把它变成y=2sin（
______）然后由y=sinx的图象先向
______平移
______个单位，再把各点的纵坐标不变，横坐标变为原来的
______倍，最后把各点的横坐标不变，纵坐标变为原来的
______倍，就可以得到y=2cos(2x+
)的图象．
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
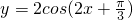的图象．可以由诱导公式先把它变成y=2sin（ ________）然后由y=sinx的图象先向 ________平移 ________个单位，再把各点的纵坐标不变，横坐标变为原来的 ________倍，最后把各点的横坐标不变，纵坐标变为原来的 ________倍，就可以得到
．
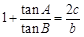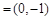，n
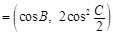，试求|m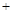
n|的最小值．
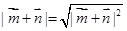表示成关于角B的函数，然后根据三角函数的知识求最小值即可.