题目内容
在△ABC中,角A,B,C所对边分别为a,b,c,且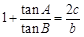 .
.
(Ⅰ)求角A;
(Ⅱ)若m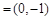 ,n
,n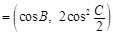 ,试求|m
,试求|m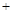 n|的最小值.
n|的最小值.
【解析】(I)把切化成弦,然后根据正弦定理,把等号右边的边的比,转化为对应的角的正弦的比,再借助诱导公式求A.
(II)根据第(I)问求出的A角,然后把C角用B角来表示,再借助向量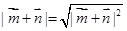 表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
【答案】
(I)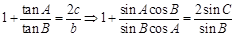 ,即
,即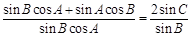 ,
,
∴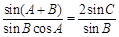 ,∴
,∴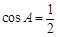 . ∵
. ∵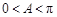 ,∴
,∴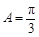 .……………(6分)
.……………(6分)
(II)m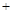 n
n 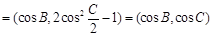 ,
,
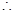 |m
|m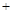 n|
n|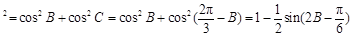 .
.
∵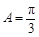 ,∴
,∴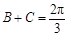 ,∴
,∴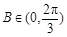 ,且
,且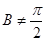 .从而
.从而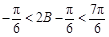 .
.
∴当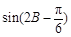 =1,即
=1,即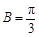 时,|m
时,|m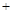 n|
n| 取得最小值
取得最小值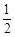 .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |