摘要:3. 已知函数. ⑴ 当.且时.求证:, ⑵ 是否存在实数..使得函数的定义域.值域都是.若存在.则求出.的值.若不存在.请说明理由. ⑶ 若存在实数数..使得函数的定义域为时.值域为.求的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_526843[举报]
已知函数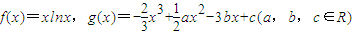 .
.
(1)若函数h(x)=f′(x)-g′(x)是其定义域上的增函数,求实数a的取值范围;
(2)若g(x)是奇函数,且g(x)的极大值是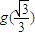 ,求函数g(x)在区间[-1,m]上的最大值;
,求函数g(x)在区间[-1,m]上的最大值;
(3)证明:当x>0时,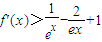 .
.
查看习题详情和答案>>
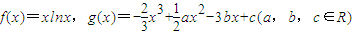 .
.(1)若函数h(x)=f′(x)-g′(x)是其定义域上的增函数,求实数a的取值范围;
(2)若g(x)是奇函数,且g(x)的极大值是
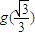 ,求函数g(x)在区间[-1,m]上的最大值;
,求函数g(x)在区间[-1,m]上的最大值;(3)证明:当x>0时,
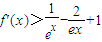 .
.查看习题详情和答案>>
已知函数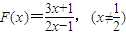 .
.
(Ⅰ)证明:F(x)+F(1-x)=3,并求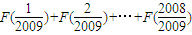 ;
;
(Ⅱ).已知等差数列{an}与{bn}的前n项和分别为Sn与Tn,且 .当m>n时,比较
.当m>n时,比较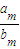 与
与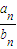 的大小;
的大小;
(Ⅲ)在(Ⅱ)条件下,已知a1=2,数列{bn}的公差为d=2.探究在数列{an}与{bn}中是否有相等的项,若有,求出这些相等项由小到大排列后得到的数列{cn}的通项公式;若没有,请说明理由.
查看习题详情和答案>>
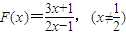 .
.(Ⅰ)证明:F(x)+F(1-x)=3,并求
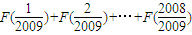 ;
;(Ⅱ).已知等差数列{an}与{bn}的前n项和分别为Sn与Tn,且
 .当m>n时,比较
.当m>n时,比较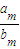 与
与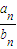 的大小;
的大小;(Ⅲ)在(Ⅱ)条件下,已知a1=2,数列{bn}的公差为d=2.探究在数列{an}与{bn}中是否有相等的项,若有,求出这些相等项由小到大排列后得到的数列{cn}的通项公式;若没有,请说明理由.
查看习题详情和答案>>
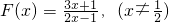 .
.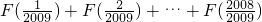 ;
;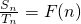 .当m>n时,比较
.当m>n时,比较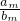 与
与 的大小;
的大小;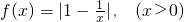 .
. .
.