题目内容
已知函数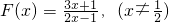 .
.
(Ⅰ)证明:F(x)+F(1-x)=3,并求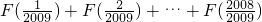 ;
;
(Ⅱ).已知等差数列{an}与{bn}的前n项和分别为Sn与Tn,且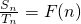 .当m>n时,比较
.当m>n时,比较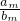 与
与 的大小;
的大小;
(Ⅲ)在(Ⅱ)条件下,已知a1=2,数列{bn}的公差为d=2.探究在数列{an}与{bn}中是否有相等的项,若有,求出这些相等项由小到大排列后得到的数列{cn}的通项公式;若没有,请说明理由.
解:(Ⅰ)因为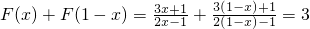 (2分)
(2分)
所以设S=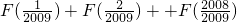 ;(1)
;(1)
S= (2)
(2)
(1)+(2)得:
=3×2008=6024,
所以S=3012(5分)
(Ⅱ)因为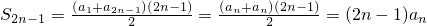
所以 .(7分)
.(7分)
所以 ;
;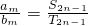
所以当m>n≥1时,

=
= ,∴
,∴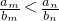 (10分)
(10分)
(Ⅲ)在(Ⅱ)条件下,当a1=2,d=2时

所以{-2+2b1=-1

d1=3
所以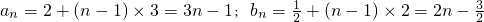 (12分)
(12分)
假若存在数列{an}中的第n项与数列{bn}中的第k项相等,
即
因为4k-1为奇数,6为偶数,所以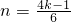 不是整数,
不是整数,
所以在数列{an}与{bn}中没有相等的项.(14分)
分析:(Ⅰ)关于f(x)+f(1-x)=3的证明,只需代入解析式验证即可.求值时,我们利用f(x)+f(1-x)=3即和为1的两个自变量对应的函数值的和为3,再看共有多少对即可,
(Ⅱ)考查等差数列前n项和与第n项的关系.由等差数列第n项的比等于前2n-1项和的比可得,然后在比较大小.
(Ⅲ)假若存在数列{an}中的第n项与数列{bn}中的第k项相等,即 ,进一步分析可得n不是整数,即可得结论.
,进一步分析可得n不是整数,即可得结论.
点评:第一问:主要查清几对即可.
第二问:两个等差数列前n项的比值与前2n-1项和的比值相等这一规律最好记住,在解决填空与选择题时可以加快速度.
第三问:要注意通项相等和第n项相等的区别.
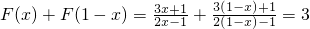 (2分)
(2分)所以设S=
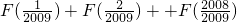 ;(1)
;(1)S=
 (2)
(2)(1)+(2)得:

=3×2008=6024,
所以S=3012(5分)
(Ⅱ)因为
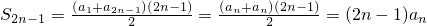
所以
 .(7分)
.(7分)所以
 ;
;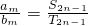
所以当m>n≥1时,

=

=
 ,∴
,∴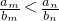 (10分)
(10分)(Ⅲ)在(Ⅱ)条件下,当a1=2,d=2时

所以{-2+2b1=-1

d1=3
所以
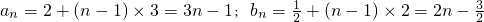 (12分)
(12分)假若存在数列{an}中的第n项与数列{bn}中的第k项相等,
即

因为4k-1为奇数,6为偶数,所以
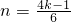 不是整数,
不是整数,所以在数列{an}与{bn}中没有相等的项.(14分)
分析:(Ⅰ)关于f(x)+f(1-x)=3的证明,只需代入解析式验证即可.求值时,我们利用f(x)+f(1-x)=3即和为1的两个自变量对应的函数值的和为3,再看共有多少对即可,
(Ⅱ)考查等差数列前n项和与第n项的关系.由等差数列第n项的比等于前2n-1项和的比可得,然后在比较大小.
(Ⅲ)假若存在数列{an}中的第n项与数列{bn}中的第k项相等,即
 ,进一步分析可得n不是整数,即可得结论.
,进一步分析可得n不是整数,即可得结论.点评:第一问:主要查清几对即可.
第二问:两个等差数列前n项的比值与前2n-1项和的比值相等这一规律最好记住,在解决填空与选择题时可以加快速度.
第三问:要注意通项相等和第n项相等的区别.

练习册系列答案
相关题目

 )在区间
)在区间 的单调性;
的单调性;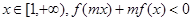 恒成立,求实数
恒成立,求实数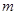 的取值范围。
的取值范围。 ,
, ;
; 是奇函数;
是奇函数; 和
和 的值,由此概括出涉及函数
的值,由此概括出涉及函数 的对所有不等于零的实数
的对所有不等于零的实数 都成立的一个等式,并加以证明
都成立的一个等式,并加以证明 .
. 上是单调函数;
上是单调函数; 上的最值.
上的最值.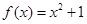
 上是单调递增的。
上是单调递增的。