题目内容
已知函数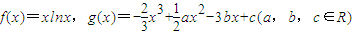 .
.(1)若函数h(x)=f′(x)-g′(x)是其定义域上的增函数,求实数a的取值范围;
(2)若g(x)是奇函数,且g(x)的极大值是
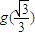 ,求函数g(x)在区间[-1,m]上的最大值;
,求函数g(x)在区间[-1,m]上的最大值;(3)证明:当x>0时,
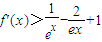 .
.
【答案】分析:(1)先对函数f(x)、g(x)进行求导表示出函数h(x)的解析式,再对函数h(x)进行求导,令导函数大于0求满足条件的a的范围即可得到答案.
(2)先根据g(x)是奇函数求出a=c=0,然后对函数g(x)进行求导,根据在x=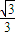 出取极值可确定b的值,从而得到函数g(x)的解析式,然后对函数g(x)求导,根据函数g(x)的单调性可解题.
出取极值可确定b的值,从而得到函数g(x)的解析式,然后对函数g(x)求导,根据函数g(x)的单调性可解题.
(3)将问题转化为证明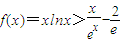 对x>0恒成立,对函数f(x)求导,根据函数f(x)的导函数确定f(x)的最小值;同样求出
对x>0恒成立,对函数f(x)求导,根据函数f(x)的导函数确定f(x)的最小值;同样求出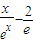 的最大值,二者比较大小可证.
的最大值,二者比较大小可证.
解答:解:(1)f'(x)=lnx+1,g'(x)=-2x2+ax-3b,所以h(x)=lnx+2x2-ax+3b+1,
由于h(x)是定义域内的增函数,故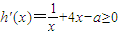 恒成立,
恒成立,
即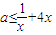 对?x>0恒成立,又
对?x>0恒成立,又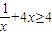 (x=2时取等号),故a∈(-∞,4].
(x=2时取等号),故a∈(-∞,4].
(2)由g(x)是奇函数,则g(x)+g(-x)=0对?x>0恒成立,从而a=c=0,
所以 ,有g'(x)=-2x2-3b.
,有g'(x)=-2x2-3b.
由g(x)极大值为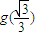 ,即
,即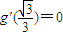 ,从而
,从而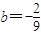 ;
;
因此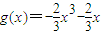 ,即
,即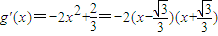 ,
,
所以函数g(x)在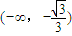 和
和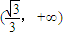 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
由g(x)=0,得x=±1或x=0,因此得到:
当-1<m<0时,最大值为g(-1)=0;
当 时,最大值为
时,最大值为 ;
;
当 时,最大值为
时,最大值为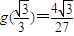 .
.
(3)问题等价于证明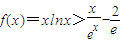 对x>0恒成立;
对x>0恒成立;
f'(x)=lnx+1,所以当 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在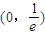 上单调减;
上单调减;
当 时,f'(x)>0,f(x)在
时,f'(x)>0,f(x)在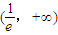 上单调增;
上单调增;
所以f(x)在(0,+∞)上最小值为 (当且仅当
(当且仅当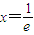 时取得)
时取得)
设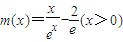 ,则
,则 ,得m(x)最大值
,得m(x)最大值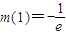 (当且仅当x=1时取得),
(当且仅当x=1时取得),
又f(x)得最小值与m(x)的最大值不能同时取到,所以结论成立.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
(2)先根据g(x)是奇函数求出a=c=0,然后对函数g(x)进行求导,根据在x=
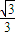 出取极值可确定b的值,从而得到函数g(x)的解析式,然后对函数g(x)求导,根据函数g(x)的单调性可解题.
出取极值可确定b的值,从而得到函数g(x)的解析式,然后对函数g(x)求导,根据函数g(x)的单调性可解题.(3)将问题转化为证明
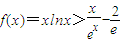 对x>0恒成立,对函数f(x)求导,根据函数f(x)的导函数确定f(x)的最小值;同样求出
对x>0恒成立,对函数f(x)求导,根据函数f(x)的导函数确定f(x)的最小值;同样求出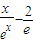 的最大值,二者比较大小可证.
的最大值,二者比较大小可证.解答:解:(1)f'(x)=lnx+1,g'(x)=-2x2+ax-3b,所以h(x)=lnx+2x2-ax+3b+1,
由于h(x)是定义域内的增函数,故
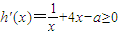 恒成立,
恒成立,即
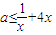 对?x>0恒成立,又
对?x>0恒成立,又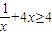 (x=2时取等号),故a∈(-∞,4].
(x=2时取等号),故a∈(-∞,4].(2)由g(x)是奇函数,则g(x)+g(-x)=0对?x>0恒成立,从而a=c=0,
所以
 ,有g'(x)=-2x2-3b.
,有g'(x)=-2x2-3b.由g(x)极大值为
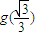 ,即
,即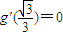 ,从而
,从而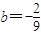 ;
;因此
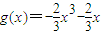 ,即
,即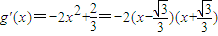 ,
,所以函数g(x)在
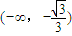 和
和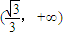 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.由g(x)=0,得x=±1或x=0,因此得到:
当-1<m<0时,最大值为g(-1)=0;
当
 时,最大值为
时,最大值为 ;
;当
 时,最大值为
时,最大值为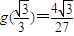 .
.(3)问题等价于证明
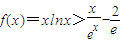 对x>0恒成立;
对x>0恒成立;f'(x)=lnx+1,所以当
 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在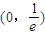 上单调减;
上单调减;当
 时,f'(x)>0,f(x)在
时,f'(x)>0,f(x)在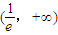 上单调增;
上单调增;所以f(x)在(0,+∞)上最小值为
 (当且仅当
(当且仅当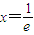 时取得)
时取得)设
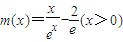 ,则
,则 ,得m(x)最大值
,得m(x)最大值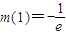 (当且仅当x=1时取得),
(当且仅当x=1时取得),又f(x)得最小值与m(x)的最大值不能同时取到,所以结论成立.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。