摘要:20. 如图.在平面直角坐标系中.过轴正方向上一点任作一直线.与抛物线相交于两点.一条垂直于轴的直线.分别与线段和直线交于点. (1)若.求的值, (2)若为线段的中点.求证:为此抛物线的切线, 的逆命题是否成立?说明理由.
网址:http://m.1010jiajiao.com/timu3_id_526549[举报]
(本题满分14分)在平面直角坐标系 中,已知圆
中,已知圆 ,
,
圆 .
.
(Ⅰ)若过点 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)圆 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ;
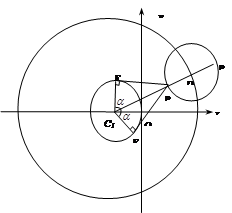
(Ⅲ)若动圆 同时平分圆
同时平分圆 的周长、圆
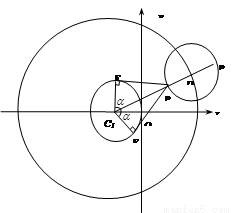
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
(本题满分14分)在平面直角坐标系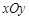 中,已知圆
中,已知圆 ,
,
圆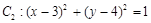 .
.
(Ⅰ)若过点 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)圆 是以1为半径,圆心在圆
是以1为半径,圆心在圆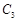 :
: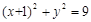 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线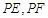 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ;
(Ⅲ)若动圆 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看习题详情和答案>>
(本题满分14分)
如图,在平面直角坐标系 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于 两点.一条垂直于
两点.一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线 交于点
交于点 .
.
(1)若 ,求
,求 的值;(5分)
的值;(5分)
(2)若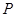 为线段
为线段 的中点,求证:
的中点,求证: 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由.(4分)

查看习题详情和答案>>
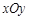 中,已知圆
中,已知圆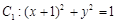 ,
,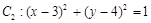 .
.
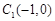 的直线
的直线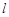 被圆
被圆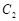 截得的弦长为
截得的弦长为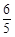 ,求直线
,求直线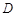 是以1为半径,圆心在圆
是以1为半径,圆心在圆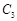 :
: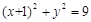 上移动的动圆 ,若圆
上移动的动圆 ,若圆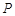 分别作圆
分别作圆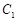 的两条切线
的两条切线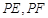 ,切点为
,切点为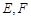 ,求
,求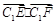 的取值范围 ;
的取值范围 ;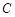 同时平分圆
同时平分圆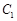 的周长、圆
的周长、圆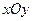 中,过
中,过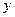 轴正方向上一点
轴正方向上一点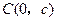 任作一直线,与抛物线
任作一直线,与抛物线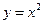 相交于
相交于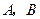 两点.一条垂直于
两点.一条垂直于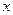 轴的直线,分别与线段
轴的直线,分别与线段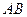 和直线
和直线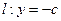 交于点
交于点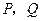 .
.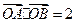 ,求
,求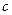 的值;(5分)
的值;(5分)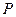 为线段
为线段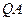 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)