题目内容
(本题满分14分)在平面直角坐标系 中,已知圆
中,已知圆 ,
,
圆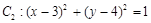 .
.
(Ⅰ)若过点 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)圆 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: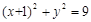 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线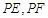 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ;
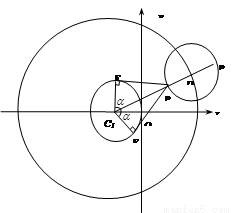
(Ⅲ)若动圆 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
【答案】
(Ⅰ) 或
或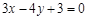
(Ⅱ)
(Ⅲ)见解析
【解析】(Ⅰ)设直线 的方程为
的方程为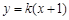 ,即
,即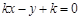 .
.
因为直线 被圆
被圆 截得的弦长为
截得的弦长为 ,而圆
,而圆 的半径为1,
的半径为1,
所以圆心 到
到 :
: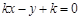 的距离为
的距离为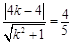 .
.
化简,得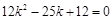 ,解得
,解得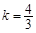 或
或 .
.
所以直线 的方程为
的方程为 或
或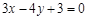 ………4分
………4分
(Ⅱ)
动圆D是圆心在定圆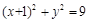 上移动,半径为1的圆
上移动,半径为1的圆
设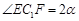 ,则在
,则在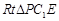 中,
中,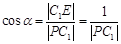 ,
,
有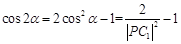 ,则
,则
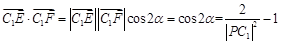
由圆的几何性质得,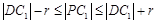 ,即
,即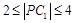 ,
,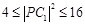
则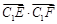 的最大值为
的最大值为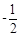 ,最小值为
,最小值为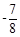 . 故
. 故 . ………9分
. ………9分
(Ⅲ)设圆心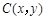 ,由题意,得
,由题意,得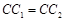 ,
,
即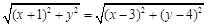 .
.
化简得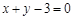 ,即动圆圆心C在定直线
,即动圆圆心C在定直线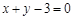 上运动.
上运动.
设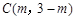 ,则动圆C的半径为
,则动圆C的半径为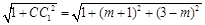 .
.
于是动圆C的方程为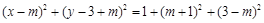 .
.
整理,得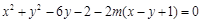 .
.
由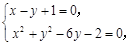 得
得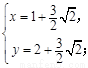 或
或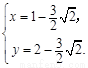
所以定点的坐标为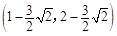 ,
,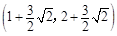 . ……14分
. ……14分

练习册系列答案
相关题目
 中,已知圆
中,已知圆 ,
, .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ; 同时平分圆
同时平分圆 的周长、圆
的周长、圆 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,且满足
,且满足
 ,求实数
,求实数 的值。
的值。 ,求
,求 的值.
的值. 的正方体
的正方体 中,
中, 是线段
是线段 的中点,底面ABCD的中心是F.
的中点,底面ABCD的中心是F. ^
^ ;
;  ;
; 的体积。
的体积。
 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
. ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程.