摘要:解 (1)由题意.2an+1-an=n.又a1=.所以2a2-a1=1.解得a2=. 同理a3=.a4=. (2)因为2an+1-an=n. 所以bn+1=an+2-an+1-1=-an+1-1=. bn=an+1-an-1=an+1-(2an+1-n)-1=n-an+1-1=2bn+1.即= 又b1=a2-a1-1=-.所以数列{bn}是以-为首项.为公比的等比数列. 得.bn=-×.Tn==3×()-. 又an+1=n-1-bn=n-1+3×().所以an=n-2+3×()n. 所以Sn=-2n+3×=+3-. 由题意.记cn=.要使数列{cn}为等差数列.只要cn+1-cn为常数. cn===+×. cn-1=+×. 则cn-cn-1=+. 故当λ=2时.cn-cn-1=为常数.即数列{}为等差数列.
网址:http://m.1010jiajiao.com/timu3_id_525769[举报]
 。
。 的最大值。
的最大值。 absinC=
absinC= ,2abcosC.
,2abcosC. .
. ,
, .
. -A)
-A) cosA+
cosA+ )≤
)≤ (
( 为实数).
为实数). 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 . ∵
. ∵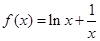 ∴
∴
 .
. 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
 时,
时, ,在
,在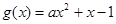 ,则
,则
 或
或 在
在 ,且
,且
 或
或
 或
或
 或
或
 或
或 . 综上
. 综上