摘要:21.对于三次函数.定义:设是函数的导函数的导数.若有实数解.则称点为函数的“拐点 .现已知,请解答下列问题: (Ⅰ)求函数的“拐点 A的坐标; (Ⅱ)求证的图象关于“拐点 A 对称;并写出对于任意的三次函数都成立的有关“拐点 的一个结论, (Ⅲ)若另一个三次函数G.且一次项系数为0.当.时.试比较与的大小.
网址:http://m.1010jiajiao.com/timu3_id_525654[举报]
对于三次函数![]() ,定义:设
,定义:设![]() 是函数
是函数![]() 的导函数
的导函数![]() 的导数,若
的导数,若![]() 有实数解
有实数解![]() ,则称点
,则称点![]() 为函数
为函数![]() 的“拐点”。现已知
的“拐点”。现已知![]() ,请解答下列问题:
,请解答下列问题:
(1)求函数![]() 的“拐点”A的坐标;
的“拐点”A的坐标;
(2)求证![]() 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
对于三次函数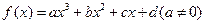 ,定义:设
,定义:设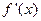 是函数
是函数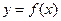 的导函数
的导函数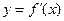 的导数,若
的导数,若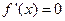 有实数解
有实数解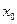 ,则称点
,则称点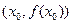 为函数
为函数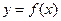 的“拐点”。现已知
的“拐点”。现已知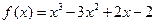 ,请解答下列问题:
,请解答下列问题:
(1)求函数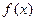 的“拐点”A的坐标;
的“拐点”A的坐标;
(2)求证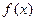 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
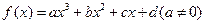 ,定义:设
,定义:设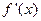 是函数
是函数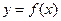 的导函数
的导函数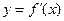 的导数,若
的导数,若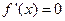 有实数解
有实数解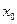 ,则称点
,则称点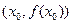 为函数
为函数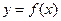 的“拐点”。现已知
的“拐点”。现已知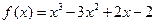 ,请解答下列问题:
,请解答下列问题:(1)求函数
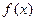 的“拐点”A的坐标;
的“拐点”A的坐标;(2)求证
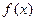 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).对于三次函数
 .
.
定义:(1)设 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称.
对称.
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)
查看习题详情和答案>>

 。
。 是函数
是函数 的导数
的导数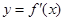 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 上的函数
上的函数 ,都有
,都有 成立,则函数
成立,则函数 ,请回答下列问题:
,请回答下列问题: 的“拐点”
的“拐点”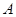 的坐标
的坐标 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)
 。
。 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 上的函数
上的函数 ,都有
,都有 成立,则函数
成立,则函数 ,请回答下列问题:
,请回答下列问题: 的“拐点”
的“拐点” 的坐标
的坐标 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)